Question

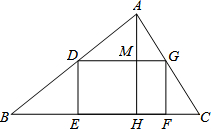如图，有一块三角形土地，它的底边BC=100m，高AH=80m．某单位要沿着底边BC修一座底面积是矩形DEFG的大楼，设DG=xm，DE=ym．
（1）求y与x之间的函数关系式．
（2）当底面DEFG是正方形时，求出正方形DEFG的面积．

Answer 1

分析：（1）两三角形相似，对应高之比等于相似比．利用此性质即可解答．
（2）利用正方形的性质代入x求解即可．

解答：解：（1）∵DG∥BC
∴△ADG∽△ABC
它们的对应高线比等于对应线段的比，
即

AM

AH

=

DG

BC

设DG=xm，DE=ym，那么AM=80-y，
∴

80-y

80

=

x

100

∴y=-

4

5

x+80；

（2）当x=y时，
x=-

4

5

x+80，
解得：x=

400

9

∴DE=

400

9

，DG=

400

9

，
∴正方形DEFG的面积为

160000

81

m²．

点评：本题主要考查利用矩形的性质得出两个角相等，进而证明两个三角形相似，再利用相似三角形的性质得出比例关系，最终求得DG或DE的长，进而求得矩形的面积．