题目内容
（2004•南宁）如图，D、E分别是⊙O的半径OA、OB上的点，CD⊥OA，CE⊥OB，CD=CE，则
与
弧长的大小关系是 ．
【答案】分析：已知CD⊥OA，CE⊥OB?∠CDO=CEO=90°，CD=CE，CO=CO?△COD≌△COE．
根据圆心角，弧，弦的关系（在同圆或等圆中，如果两个圆心角、两条弧、两条弦中只要有一组量相等，那么它们所对应的其余各组量都分别相等．）可得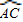
=
．
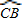解答：解：∵CD⊥OA，CE⊥OB
∴∠CDO=∠CEO=90°，CD=CE，CO=CO
∴△COD≌△COE
∴
=
．
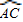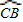点评：本题考查的是圆心角，弧，弦的关系以及全等三角形的判定（AAS），难度一般．
根据圆心角，弧，弦的关系（在同圆或等圆中，如果两个圆心角、两条弧、两条弦中只要有一组量相等，那么它们所对应的其余各组量都分别相等．）可得
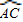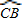=．解答：解：∵CD⊥OA，CE⊥OB
∴∠CDO=∠CEO=90°，CD=CE，CO=CO
∴△COD≌△COE
∴
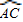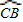=．点评：本题考查的是圆心角，弧，弦的关系以及全等三角形的判定（AAS），难度一般．
练习册系列答案
孟建平小学滚动测试系列答案
相关题目
与
弧长的大小关系是 ．
