题目内容
（2008•台州）如图，正方形网格中的每个小正方形的边长都是1，每个小正方形的顶点叫做格点．△ABO的三个顶点A，B，O都在格点上．（1）画出△ABO绕点O逆时针旋转90°后得到的三角形；
（2）求△ABO在上述旋转过程中所扫过的面积．
【答案】分析：由网格图知，OB=4，AB=OA=2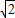
，作B′O⊥OB，且OB′=OB，A′O⊥OA，且OA′=OA，△AOB所扫过的面积是由一个圆心角为90度的扇形与△OAB的面积之和，求得即可．
解答：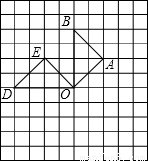
解：（1）画图正确（如图）．
（2）△AOB所扫过的面积是：S=S扇形DOB+S△AOB=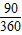
π×42+4=4π+4．
点评：本题利用了等腰直角三角形的性质，三角形的面积公式及扇形的面积公式．
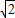，作B′O⊥OB，且OB′=OB，A′O⊥OA，且OA′=OA，△AOB所扫过的面积是由一个圆心角为90度的扇形与△OAB的面积之和，求得即可．解答：
解：（1）画图正确（如图）．（2）△AOB所扫过的面积是：S=S扇形DOB+S△AOB=
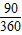π×42+4=4π+4．点评：本题利用了等腰直角三角形的性质，三角形的面积公式及扇形的面积公式．
练习册系列答案
黄冈360度定制密卷系列答案
阳光考场单元测试卷系列答案
名校联盟冲刺卷系列答案
名校提分一卷通系列答案
相关题目
，点P是边BC上的动点（点P不与点B，点C重合），过点P作直线PQ∥BD，交CD边于Q点，再把△PQC沿着动直线PQ对折，点C的对应点是R点，设CP的长度为x，△PQR与矩形ABCD重叠部分的面积为y．
．
，点P是边BC上的动点（点P不与点B，点C重合），过点P作直线PQ∥BD，交CD边于Q点，再把△PQC沿着动直线PQ对折，点C的对应点是R点，设CP的长度为x，△PQR与矩形ABCD重叠部分的面积为y．
．
，点P是边BC上的动点（点P不与点B，点C重合），过点P作直线PQ∥BD，交CD边于Q点，再把△PQC沿着动直线PQ对折，点C的对应点是R点，设CP的长度为x，△PQR与矩形ABCD重叠部分的面积为y．
．