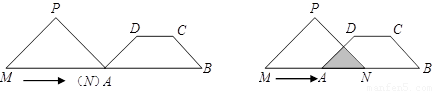题目内容
在等腰梯形![]() 中,
中,![]() ,一条直线
,一条直线![]() 与下底
与下底![]() 相交于点
相交于点![]() ,且直线
,且直线![]() 将等腰梯形
将等腰梯形![]() 的周长平分。
的周长平分。
(1)如图,若直线![]() 与腰
与腰![]() 相交于点
相交于点![]() ,设
,设![]() 为
为![]() ,试用含
,试用含![]() 的代数式表示
的代数式表示![]() 的面积;
的面积;
(2)是否存在直线![]() 将等腰梯形
将等腰梯形![]() 的周长和面积同时平分?若存在,指出符合要求的所有直线的特征;若不存在,请说明理由。
的周长和面积同时平分?若存在,指出符合要求的所有直线的特征;若不存在,请说明理由。

解:(1)过点![]() 作
作![]() ,垂足为
,垂足为![]() ;过点
;过点![]() 作
作![]() ,垂足为
,垂足为![]()
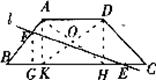
由题意知,![]() 的周长为12,
的周长为12,![]() 。
。
∴![]()
![]()
![]() ,即
,即![]() ,
,
∴ ![]()
∴![]() 。
。
(2)存在。
①当![]() 与腰
与腰![]() 相交时,
相交时,
![]() ,
,
∴由(1)得![]() 解这个方程,得
解这个方程,得![]()
由题意知,![]() ,故只取
,故只取![]() 。
。
![]() 当
当![]() 时,
时,![]() 故直线
故直线![]() 过点
过点![]() ,且
,且![]() 。
。
②当![]() 与腰
与腰![]() 相交时,由对称性知,
相交时,由对称性知,![]() 过点
过点![]() ,且
,且![]() 。
。
③当![]() 与
与![]() 相交时,作
相交时,作![]() ,垂足为
,垂足为![]() ,连接
,连接![]() ,
,![]() ,其交点为
,其交点为![]() ,
,
由对称性知。过![]() 点的直线
点的直线![]() 均符合条件。
均符合条件。
综上所述。过点![]() 且与下底相交的直线
且与下底相交的直线![]() 均能将等腰梯形
均能将等腰梯形![]() 的周长和面积同时平分。
的周长和面积同时平分。

练习册系列答案
相关题目
 移动
移动 时,等腰直角三角形
时,等腰直角三角形 重
重 ,求
,求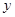 与
与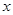 之间的函数关系式;
之间的函数关系式;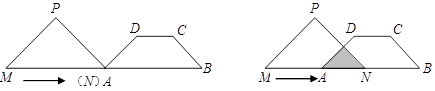
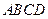 中,
中,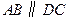 ,
,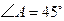 ,
,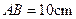 ,
, .等腰直角三角形
.等腰直角三角形 的斜边
的斜边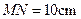 ,
,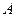 点与
点与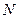 点重合,
点重合,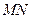 和
和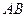 在一条直线上,设等腰梯形
在一条直线上,设等腰梯形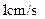 的速度向右移动,直到点
的速度向右移动,直到点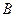 重合为止.
重合为止.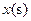 时,等腰直角三角形
时,等腰直角三角形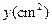 ,求
,求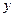 与
与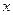 之间的函数关系式;
之间的函数关系式;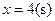 时,求等腰直角三角形
时,求等腰直角三角形
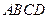 中,
中, ,
, ,
,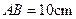 ,
, .等腰直角三角形
.等腰直角三角形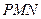 的斜边
的斜边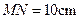 ,
,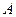 点与
点与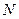 点重合,
点重合, 和
和 在一条直线上,设等腰梯形
在一条直线上,设等腰梯形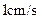 的速度向右移动,直到点
的速度向右移动,直到点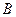 重合为止.
重合为止.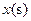 时,等腰直角三角形
时,等腰直角三角形 ,求
,求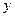 与
与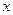 之间的函数关系式;
之间的函数关系式;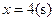 时,求等腰直角三角形
时,求等腰直角三角形
 中,
中,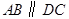 ,
,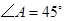 ,
,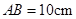 ,
,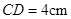 .等腰直角三角形
.等腰直角三角形 的斜边
的斜边 ,
,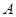 点与
点与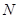 点重合,
点重合,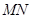 和
和 在一条直线上,设等腰梯形
在一条直线上,设等腰梯形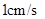 的速度向右移动,直到点
的速度向右移动,直到点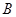 重合为止.
重合为止. 时,等腰直角三角形
时,等腰直角三角形 ,求
,求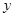 与
与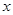 之间的函数关系式;
之间的函数关系式; 时,求等腰直角三角形
时,求等腰直角三角形