题目内容
已知：如图，⊙O2过⊙O1的圆心O1且与⊙O1内切于点P．弦AB切⊙O2于点C，PA、PB分别与⊙
O2交于D、E两点，延长PC交⊙O1于点F．求证：
（1）BC2=BE•BP；
（2）∠1=∠2；
（3）CF2=BE•AP．
分析：（1）连接CE，利用弦切角定理易得∠2=∠BCE，再加一组公共角，易证△BCE∽△BPC，可得比例线段，从而可证；
（2）作⊙O1与⊙O2的公切线PM，利用弦切角定理、结合三角形外角性质易证∠1=∠BCE，再利用弦切角定理可证∠1=∠2；
（3）连接O1P、O1E、O1C，由于O1P是小圆的直径，那么∠O1CP=90°，利用垂径定理，可证CF=CP①，同理可证BE=EP②，利用弦切角定理易得∠ACP=∠ECP，结合（2）中的结论，易证△ACP∽△CEP，可得比例线段，再把①②代入，化简即可得证．
（2）作⊙O1与⊙O2的公切线PM，利用弦切角定理、结合三角形外角性质易证∠1=∠BCE，再利用弦切角定理可证∠1=∠2；
（3）连接O1P、O1E、O1C，由于O1P是小圆的直径，那么∠O1CP=90°，利用垂径定理，可证CF=CP①，同理可证BE=EP②，利用弦切角定理易得∠ACP=∠ECP，结合（2）中的结论，易证△ACP∽△CEP，可得比例线段，再把①②代入，化简即可得证．
解答：
证明：（1）连接CE，（1分）
∵BC是⊙O2的切线，
∴∠2=∠BCE，（3分）
又∵∠B=∠B，
∴△BCE∽△BPC，（5分）
∴
=
，
∴BC2=BE•BP；（6分）
（2）作⊙O1与⊙O2的公切线PM，（7分）
∵∠MPC=∠CEP，∠MPA=∠B，（8分）
∴∠1=∠MPC-∠MPA=∠CEP-∠B，（9分）
又∠CEP-∠B=∠BCE，
∴∠1=∠BCE，（10分）
又∵AB切⊙O2于C，
∴∠BCE=∠2，（11分）
∴∠1=∠2；（12分）
（3）连接O1P、O1E、O1C，
∵P是切点，
∴O1P是直径，（13分）
∴O1E⊥PB，（14分）
∴BE=EP，①（15分）
同理，FC=PC，②（16分）
在△ACP和△CEP中，∵AC是切线，
∴∠ACP=∠CEP，（17分）
又∠1=∠2，
∴△ACP∽△CEP，（18分）
∴
=
，
∴CP2=AP•EP，（19分）
将①、②式代入，得CF2=BE•AP．（20分）
证明：（1）连接CE，（1分）∵BC是⊙O2的切线，
∴∠2=∠BCE，（3分）
又∵∠B=∠B，
∴△BCE∽△BPC，（5分）
∴
| BE |
| BC |
| BC |
| BP |
∴BC2=BE•BP；（6分）
（2）作⊙O1与⊙O2的公切线PM，（7分）
∵∠MPC=∠CEP，∠MPA=∠B，（8分）
∴∠1=∠MPC-∠MPA=∠CEP-∠B，（9分）
又∠CEP-∠B=∠BCE，
∴∠1=∠BCE，（10分）
又∵AB切⊙O2于C，
∴∠BCE=∠2，（11分）
∴∠1=∠2；（12分）
（3）连接O1P、O1E、O1C，
∵P是切点，
∴O1P是直径，（13分）
∴O1E⊥PB，（14分）
∴BE=EP，①（15分）
同理，FC=PC，②（16分）
在△ACP和△CEP中，∵AC是切线，
∴∠ACP=∠CEP，（17分）
又∠1=∠2，
∴△ACP∽△CEP，（18分）
∴
| AP |
| CP |
| CP |
| EP |
∴CP2=AP•EP，（19分）
将①、②式代入，得CF2=BE•AP．（20分）
点评：本题主要利用了弦切角定理、相似三角形的判定和性质、垂径定理、等量代换等性质．
练习册系列答案
相关题目
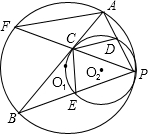已知：如图，⊙O2过⊙O1的圆心O1，且与⊙O1内切于点P，弦AB切⊙O2于点C，PA、PB分别与⊙O2交于D、E，延长PC交⊙O1于点F，连接CD、CE、AF．
