题目内容
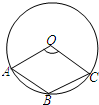如图，四边形有三个顶点在⊙O上，一个顶点在圆心O，且∠O=100°，则∠B=
- A.130°
- B.100°
- C.80°
- D.50°
A
分析：在优弧AC上任意取一点M，由∠O的度数，根据圆周角定理，求出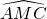
所对的圆心角，而所求的角刚好是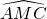所对的圆周角，根据同弧所对的圆周角等于所对圆心角的一半即可求出∠B的度数．
解答：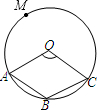
解：在优弧AC上取一点M，
由∠O=100°，得到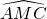所对的圆心角∠AOC=360°-100°=260°（大于平角的角），
又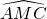所对的圆周角为∠B，
则∠B=
∠AOC=×260°=130°．
故选A．
点评：求出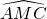所对的圆心角是解本题的关键，同时学生应掌握同弧或等弧所对的圆心角等于圆周角的2倍．
分析：在优弧AC上任意取一点M，由∠O的度数，根据圆周角定理，求出
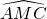所对的圆心角，而所求的角刚好是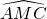所对的圆周角，根据同弧所对的圆周角等于所对圆心角的一半即可求出∠B的度数．解答：
解：在优弧AC上取一点M，由∠O=100°，得到
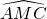所对的圆心角∠AOC=360°-100°=260°（大于平角的角），又
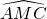所对的圆周角为∠B，则∠B=
∠AOC=×260°=130°．故选A．
点评：求出
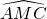所对的圆心角是解本题的关键，同时学生应掌握同弧或等弧所对的圆心角等于圆周角的2倍． 
练习册系列答案
相关题目
