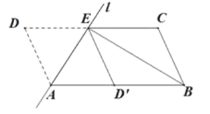
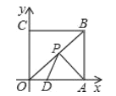
[题目]如图.正方形OABC的边长为6.点A.C分别在x轴.y轴的正半轴上.点D(2.0)在OA上.P是OB上一动点.则PA+PD的最小值为．题目和参考答案——青夏教育精英家教网—

题目内容

【题目】如图，正方形OABC的边长为6，点A、C分别在x轴，y轴的正半轴上，点D（2，0）在OA上，P是OB上一动点，则PA+PD的最小值为__．

【答案】

【解析】

过D点作关于OB的对称点D′，连接D′A交OB于点P，由两点之间线段最短可知D′A即为PA+PD的最小值，
由正方形的性质可求出D′点的坐标，再根据OA=6可求出A点的坐标，利用两点间的距离公式即可求出D′A的值．

解：过D点作关于OB的对称点D′，连接D′A交OB于点P，由两点之间线段最短可知D′A即为PA+PD的最小值，

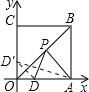
∵D（2，0），四边形OABC是正方形，
∴D′点的坐标为（0，2），A点坐标为（6，0），
∴D′A=，即PA+PD的最小值为2．
故答案为：2．

练习册系列答案

名校课堂系列答案

（1）根据图中信息求出m=　　，n=　　；

（2）请你帮助他们将这两个统计图补全；

（3）根据抽样调查的结果，请估算全校2000名学生中，大约有多少人最认可“微信”这一新生事物？

（4）已知A、B两位同学都最认可“微信”，C同学最认可“支付宝”D同学最认可“网购”从这四名同学中抽取两名同学，请你通过树状图或表格，求出这两位同学最认可的新生事物不一样的概率．

（1）求每辆A型车和B型车的售价各为多少元．

（2）甲公司拟向该店购买A，B两种型号的新能源汽车共6辆，购车费不超过84万元．问最多可以购买多少辆B型号的新能源汽车？

（1）请在数轴上表示点 A，B 位置，a= ，b= ；

（2）请用含 x 的代数式表示 CB= ；

（3）若点 C 在点 B 的左侧，且 CB=8，点 A 以每秒 2 个单位长度的速度沿数轴向右运动，当 AC=2AB时，求点 A 移动的时间．

【题目】如图，将沿过点的直线折叠，使点落到边上的处，折痕交边于点，连接.

（1）求证：四边形是平行四边形；

（2）若平分，求证：.

【题目】【题目】如图①，一次函数 y＝ x - 2 的图像交 x 轴于点 A，交 y 轴于点 B，二次函数 y＝ x2 bx c的图像经过 A、B 两点，与 x 轴交于另一点 C．

（1）求二次函数的关系式及点 C 的坐标；

（2）如图②，若点 P 是直线 AB 上方的抛物线上一点，过点 P 作 PD∥x 轴交 AB 于点 D，PE∥y 轴交 AB 于点 E，求 PD＋PE 的最大值；

（3）如图③，若点 M 在抛物线的对称轴上，且∠AMB＝∠ACB，求出所有满足条件的点 M的坐标．

① ② ③

图1中有_ __个三角形，图2中有 __个三角形，图3 中有 __个三角形；

按上面的方法继续下去，第个图形有________个三角形；(用含的式子表示)

当时，图形中有多少个三角形？

【题目】某自行车厂一周计划生产辆，自行车厂平均每天生产自行车辆，由于各种原因实际每天生产量与计划每天生产量相比有出入，下表是某周的自行车生产情况(超计划生产量为正、不足计划生产量为负，单位：辆)

星期	一	二	三	四	五	六	日
增将

根据记录可知前三天共生产自行车辆；

产量最多的一天比产量最少的一天多生产辆；

若该厂实行按生产的自行车数量的多少计工资(即计件工资制)．如果每生产一辆自行车可得人民币元，那么该厂工人这一周的工资总额是多少元．

试题分类