题目内容
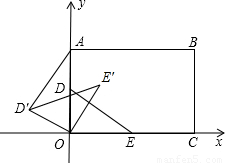
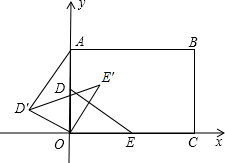 已知,如图所示,矩形OABC在平面直角坐标系中,矩形各顶点分别为O(0,0),A(0,6),B(8,6),C(8,0).点D(0,3)在OA上,点E(4,0)在OC上,连接DE,将△DOE绕O点逆时针旋转,旋转角为α(0°<α<360°),得到△D′OE′,连接AD′,当∠AD′O=90°时,
已知,如图所示,矩形OABC在平面直角坐标系中,矩形各顶点分别为O(0,0),A(0,6),B(8,6),C(8,0).点D(0,3)在OA上,点E(4,0)在OC上,连接DE,将△DOE绕O点逆时针旋转,旋转角为α(0°<α<360°),得到△D′OE′,连接AD′,当∠AD′O=90°时,
(1)旋转角α等于______度;
(2)求D′、E′的坐标.
解:(1)如图①,
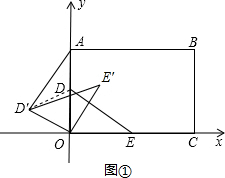
连接D′D,
∵当∠AD′O=90°时,
∵点D(0,3)在OA上,A(0,6),
∴DD′=AD=DO= AO=3,
AO=3,
∵DO=D′O=3,
∴DO=D′O=DD′,
∴∠DOD′=60°,
如图②,∵当∠AD″O=90°时,
∵点D(0,3)在OA上,A(0,6),
∴DD″=AD=DO= AO=3,
AO=3,
∵DO=D″O=3,
∴DO=D″O=DD″,
∴∠DOD″=60°,
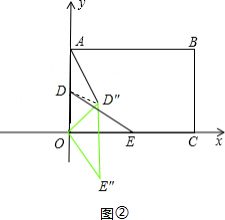
将△DOE绕O点逆时针旋转,旋转角为:60°或300°,
故答案为:60或300;
(2)如图1,作D′F⊥x轴于F,E′H⊥x轴于H,

∵∠AD′O=90°,OA=6,OD′=3,①
∴∠D′AO=30°,
∴∠D′OF=30°,∠E′OH=60°,
∵OD′=OD=3,OE′=OE=4,
∴D′F= ,FO=
,FO= ,OH=2,E
,OH=2,E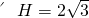 ,
,
∴D′(- ,
, ),E′(2,2
),E′(2,2 ),
),
如图2,当旋转300°时,D′与D″关于y轴对称,纵坐标相等,E′与E″关于x轴对称,进而得出答案.
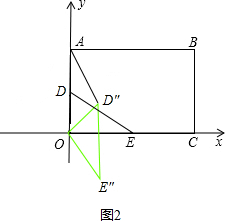
D″( ,
, ),E″(2,-2
),E″(2,-2 ).
).
综上所述:D′、E′的坐标为:D′(- ,
, ),E′(2,2
),E′(2,2 ),D″(
),D″( ,
, ),E″(2,-2
),E″(2,-2 ).
).
分析:(1)根据将△DOE绕O点逆时针旋转,利用当∠AD′O=90°时,可以得出两种情况,利用等边三角形的判定,结合图形求出即可;
(2)利用(1)中两种情况,分别利用锐角三角函数关系求出D′、E′的坐标即可.
点评:此题主要考查了图象的旋转,利用旋转的不确定性得出两种情况进而得出是解题关键.

连接D′D,
∵当∠AD′O=90°时,
∵点D(0,3)在OA上,A(0,6),
∴DD′=AD=DO=
 AO=3,
AO=3,∵DO=D′O=3,
∴DO=D′O=DD′,
∴∠DOD′=60°,
如图②,∵当∠AD″O=90°时,
∵点D(0,3)在OA上,A(0,6),
∴DD″=AD=DO=
 AO=3,
AO=3,∵DO=D″O=3,
∴DO=D″O=DD″,
∴∠DOD″=60°,

将△DOE绕O点逆时针旋转,旋转角为:60°或300°,
故答案为:60或300;
(2)如图1,作D′F⊥x轴于F,E′H⊥x轴于H,

∵∠AD′O=90°,OA=6,OD′=3,①
∴∠D′AO=30°,
∴∠D′OF=30°,∠E′OH=60°,
∵OD′=OD=3,OE′=OE=4,
∴D′F=
 ,FO=
,FO= ,OH=2,E
,OH=2,E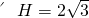 ,
,∴D′(-
 ,
, ),E′(2,2
),E′(2,2 ),
),如图2,当旋转300°时,D′与D″关于y轴对称,纵坐标相等,E′与E″关于x轴对称,进而得出答案.

D″(
 ,
, ),E″(2,-2
),E″(2,-2 ).
).综上所述:D′、E′的坐标为:D′(-
 ,
, ),E′(2,2
),E′(2,2 ),D″(
),D″( ,
, ),E″(2,-2
),E″(2,-2 ).
).分析:(1)根据将△DOE绕O点逆时针旋转,利用当∠AD′O=90°时,可以得出两种情况,利用等边三角形的判定,结合图形求出即可;
(2)利用(1)中两种情况,分别利用锐角三角函数关系求出D′、E′的坐标即可.
点评:此题主要考查了图象的旋转,利用旋转的不确定性得出两种情况进而得出是解题关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 已知,如图所示,矩形OABC在平面直角坐标系中,矩形各顶点分别为O(0,0),A(0,6),B(8,6),C(8,0).点D(0,3)在OA上,点E(4,0)在OC上,连接DE,将△DOE绕O点逆时针旋转,旋转角为α(0°<α<360°),得到△D′OE′,连接AD′,当∠AD′O=90°时,
已知,如图所示,矩形OABC在平面直角坐标系中,矩形各顶点分别为O(0,0),A(0,6),B(8,6),C(8,0).点D(0,3)在OA上,点E(4,0)在OC上,连接DE,将△DOE绕O点逆时针旋转,旋转角为α(0°<α<360°),得到△D′OE′,连接AD′,当∠AD′O=90°时,