Question

【题目】“边疆宣讲团”从招待所出发，动身前往某边防哨所去为哨所官兵宣讲“十九大”精神.若按照他们出发时的速度匀速直线行进，则刚好在约定的时间准点到达哨所; 可天有不测风云! 因道路交通事故，他们中途被迫停留了半小时; 为按约定时

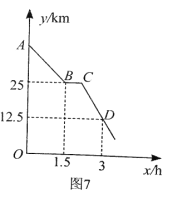
间准点到达哨所，他们后来加快速度但仍保持匀速直线行进，结果正好准点到达哨所.如图7，是他们离哨所的距离y(km)与所用时间x(h)之间的部分函数图象.根据图象，解答下列问题:

(1)求CD所在直线的表达式;

(2)求招待所离哨所的距离.

Answer 1

【答案】（1）CD的解析式为：y=-12.5+50；（2）招待所与哨所之间距离为40km

【解析】试题分析：（1）根据点C、D的坐标利用待定系数法，即可求出CD所在直线的表达式；

（2）利用一次函数图象上点的坐标特征可得出原计划4小时到达，结合点B的坐标利用待定系数法，即可求出AB所在直线的表达式，代入x=0即可得出点A的坐标，此题得解．

试题解析：（1）设CD所在直线的表达式为y=kx+b（k≠0），

将点C（2，25）、D（3，12.5）代入y=kx+b，

得，解得：，

∴CD所在直线的表达式为y=﹣12.5x+50．

（2）当y=0时，有﹣12.5x+50=0，

解得：x=4，

∴原计划4小时到达．

设AB所在直线的表达式为y=mx+n（m≠0），

将点（1.5，25）、（4，0）代入y=mx+n，

得，解得：，

∴AB所在直线的表达式为y=﹣10x+40．

当x=0时，y=﹣10x+40=40，

∴点A的坐标为（0，40），

∴招待所离哨所的距离为40km．