题目内容
 阅读下面材料:
阅读下面材料:
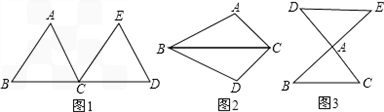
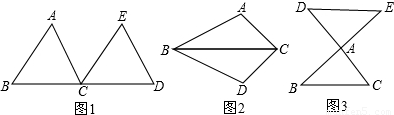
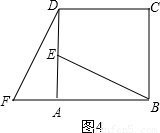
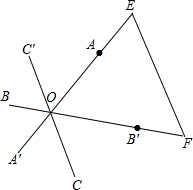
如图1,已知线段AB、CD相交于点O,且AB=CD,请你利用所学知识把线段AB、CD转移到同一三角形中.
小强同学利用平移知识解决了此问题,具体做法:
如图2,延长OD至点E,使DE=CO,延长OA至点F,使AF=OB,连接EF,则△OEF为所求的三角形.
请你仔细体会小强的做法,探究并解答下列问题:
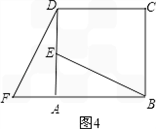
如图3,长为2的三条线段AA′,BB′,CC′交于一点O,并且∠B′OA=∠C′OB=∠A′OC=60°;
(1)请你把三条线段AA′,BB′,CC′转移到同一三角形中.(简要叙述画法)
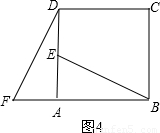
(2)连接AB′、BC′、CA′,如图4,设△AB′O、△BC′O、△CA′O的面积分别为S1、S2、S3,则S1+S2+S3______ (填“>”或“<”或“=”).
(填“>”或“<”或“=”).
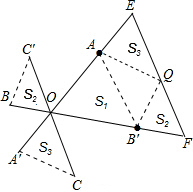
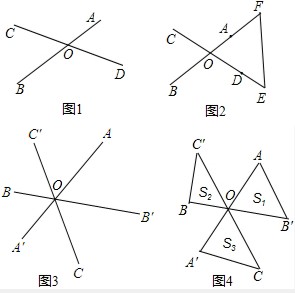
 解:(1)如图所示:
解:(1)如图所示:画法:①延长OA至点E,使AE=A′O;
②延长OB′至点F,使B′F=OB;
③连接EF,则△OEF为所求的三角形.
(2)∵长为2的三条线段AA′,BB′,CC′交于一点O,
并且∠B′OA=∠C′OB=∠A′OC=60°;
∴△OEF为边长为2的等边三角形,
∴S△OEF=
 ×2×
×2× =
= ,
,在EF上截取EQ=CO,则QF=C′O,
∴可得△A′CO≌△QEA,△B′FQ≌△OBC′,
如图所示:
则S1+S2+S3<S△EOF=
 .
.故答案为:<.
分析:(1)根据材料得出延长OA至点E,使AE=A′O;延长OB′至点F,使B′F=OB;连接EF,则△OEF为所求;
(2)根据平移的性质首先得出S△OEF=
 ×2×
×2× =
= ,再利用图象得出S1+S2+S3<S△EOF.
,再利用图象得出S1+S2+S3<S△EOF.点评:此题主要考查了图形的平移以及等边三角形的性质和全等三角形的判定等知识,根据图象得出S1+S2+S3<S△EOF是解题关键.

练习册系列答案
相关题目


 (2012•房山区一模)阅读下面材料:
(2012•房山区一模)阅读下面材料: