题目内容
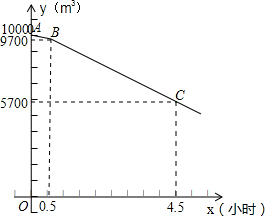
平安加气站某日8:00的储气量为10000立方米.从8:00开始,3把加气枪同时以每车20立方米的加气量,依次给在加气站排队等候的若干辆车加气.8:30时,为缓解排队压力,又增开了2把加气枪.假设加气过程中每把加气枪加气的速度是匀速的,在不关闭加气枪的情况下,加气站的储气量y(立方米)与x时间(小时)的函数关系用图中的折线ABC所示.
(1)分别求出8:00-8:30及8:30之后加气站的储气量y(立方米)与时间x(小时)的函数关系式.
(2)前30辆车能否在当天8:42之前加完气?
(3)若前n辆车按上述方式加气,它们加完气的时间要比不增开加气枪加完气的时间提前1个小时,求n的值.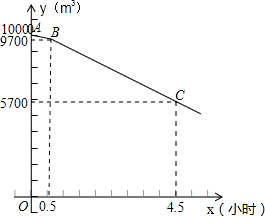
解:(1)设8:00-8:30加气站的储气量y(立方米)与时间x(小时)的函数关系式是y1=kx+b,
根据图象得出直线过(0,10000)和(0.5,9700),代入得: ,
,
解得:k=-600,b=10000,
∴8:00-8:30加气站的储气量y(立方米)与时间x(小时)的函数关系式是y1=-600x+10000;
设8:30之后加气站的储气量y(立方米)与时间x(小时)的函数关系式是y2=ax+c,
根据图象得出直线过(4.5,5700)和(0.5,9700),代入得: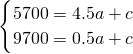 ,
,
解得:a=-1000,c=10200,
∴8:00-8:30加气站的储气量y(立方米)与时间x(小时)的函数关系式是y2=-1000x+10200;
(2)30辆车需消耗气体为30×20=600(立方米);
10000-600=9400,
由图可知,在8:30之前无法加完;
把y=9400代入y=10200-1000x,解得x=0.8(小时);
∵0.8×60=48>42,
∴当天8:42之前无法加完气;
(3)∵n辆车需加气20n立方米,
把y=10000-20n代入y1=-600x+10000得:x= ,
,
把y=10000-20n代入y2=-1000x+10200得:x= +
+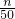 ,
,
∴ -(
-( +
+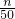 )=1,
)=1,
解得:n=90.
分析:(1)设8:00-8:30加气站的储气量y(立方米)与时间x(小时)的函数关系式是y1=kx+b,把(0,10000)和(0.5,9700)代入得出方程组 ,求出方程组的解即可;设8:30之后加气站的储气量y(立方米)与时间x(小时)的函数关系式是y2=ax+c,把(4.5,5700)和(0.5,9700)代入求出即可.
,求出方程组的解即可;设8:30之后加气站的储气量y(立方米)与时间x(小时)的函数关系式是y2=ax+c,把(4.5,5700)和(0.5,9700)代入求出即可.
(2)求出30辆车需消耗气体为600立方米,根据图象得出在8:30之前无法加完;把y=9400代入y=10200-1000x,求出x=48分钟,和42分钟比较即可.
(3)求出n辆车需加气20n立方米,分别y=10000-20n代入y1=-600x+10000和y2=-1000x+10200,求出x的值,即可得出方程 -(
-( +
+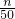 )=1,求出方程的解即可.
)=1,求出方程的解即可.
点评:本题考查了一次函数的应用,主要考查学生分析问题和解决问题的能力,题目比较好,但有一定的难度.
根据图象得出直线过(0,10000)和(0.5,9700),代入得:
 ,
,解得:k=-600,b=10000,
∴8:00-8:30加气站的储气量y(立方米)与时间x(小时)的函数关系式是y1=-600x+10000;
设8:30之后加气站的储气量y(立方米)与时间x(小时)的函数关系式是y2=ax+c,
根据图象得出直线过(4.5,5700)和(0.5,9700),代入得:
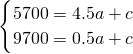 ,
,解得:a=-1000,c=10200,
∴8:00-8:30加气站的储气量y(立方米)与时间x(小时)的函数关系式是y2=-1000x+10200;
(2)30辆车需消耗气体为30×20=600(立方米);
10000-600=9400,
由图可知,在8:30之前无法加完;
把y=9400代入y=10200-1000x,解得x=0.8(小时);
∵0.8×60=48>42,
∴当天8:42之前无法加完气;
(3)∵n辆车需加气20n立方米,
把y=10000-20n代入y1=-600x+10000得:x=
 ,
,把y=10000-20n代入y2=-1000x+10200得:x=
 +
+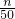 ,
,∴
 -(
-( +
+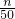 )=1,
)=1,解得:n=90.
分析:(1)设8:00-8:30加气站的储气量y(立方米)与时间x(小时)的函数关系式是y1=kx+b,把(0,10000)和(0.5,9700)代入得出方程组
 ,求出方程组的解即可;设8:30之后加气站的储气量y(立方米)与时间x(小时)的函数关系式是y2=ax+c,把(4.5,5700)和(0.5,9700)代入求出即可.
,求出方程组的解即可;设8:30之后加气站的储气量y(立方米)与时间x(小时)的函数关系式是y2=ax+c,把(4.5,5700)和(0.5,9700)代入求出即可.(2)求出30辆车需消耗气体为600立方米,根据图象得出在8:30之前无法加完;把y=9400代入y=10200-1000x,求出x=48分钟,和42分钟比较即可.
(3)求出n辆车需加气20n立方米,分别y=10000-20n代入y1=-600x+10000和y2=-1000x+10200,求出x的值,即可得出方程
 -(
-( +
+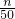 )=1,求出方程的解即可.
)=1,求出方程的解即可.点评:本题考查了一次函数的应用,主要考查学生分析问题和解决问题的能力,题目比较好,但有一定的难度.

练习册系列答案
相关题目
平安加气站某日的储气量为10000立方米.假设加气过程中每把加气枪均以每小时200立方米的速度为汽车加气.设加气站的储气量为y(立方米),加气总时间为x(小时)(加气期间关闭加气枪的时间忽略不计).从7︰00开始,加气站加气枪的使用数量如下表所示:
| 时间段 | 7︰00—7︰30] | 7︰30—8︰00 | 8︰00以后 |
| 加气枪使用︰数量 (单位:把) | 3 | 5 | 6 |
1.分别求出7︰00—7︰30及8︰00之后加气站的储气量y(立方米)与时间x(小时)的函数关系式.
2.若每辆车的加气量均为20立方米,请通过计算说明前50辆车能否在当天8︰00之前加完气.
平安加气站某日的储气量为10000立方米.假设加气过程中每把加气枪均以每小时200立方米的速度为汽车加气.设加气站的储气量为y(立方米),加气总时间为x(小时)(加气期间关闭加气枪的时间忽略不计).从7︰00开始,加气站加气枪的使用数量如下表所示:
|
时间段 |
7︰00—7︰30] |
7︰30—8︰00 |
8︰00以后 |
|
加气枪使用︰数量 (单位:把) |
3 |
5 |
6 |
1.分别求出7︰00—7︰30及8︰00之后加气站的储气量y(立方米)与时间x(小时)的函数关系式.
2.若每辆车的加气量均为20立方米,请通过计算说明前50辆车能否在当天8︰00之前加完气.