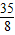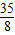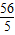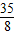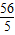题目内容
AB是一圆的直径，C，D是圆周上的两点．已知AC=7，BC=24，AD=15，求BD=（ ）A．16
B．20
C．
D．
【答案】分析：根据直径所对的圆周角是直角，得∠ACB=∠ADB=90°，再根据勾股定理分别求得AB，BD的长即可．
解答：
解：∵AB是直径
∴∠ACB=∠ADB=90°
∵AC=7，BC=24
∴AB=25
∵AD=15
∴BD=20．
故选B．
点评：考查了圆周角定理的推论以及勾股定理．
解答：
解：∵AB是直径∴∠ACB=∠ADB=90°
∵AC=7，BC=24
∴AB=25
∵AD=15
∴BD=20．
故选B．
点评：考查了圆周角定理的推论以及勾股定理．
练习册系列答案
名校课堂系列答案
相关题目
AB是一圆的直径，C，D是圆周上的两点．已知AC=7，BC=24，AD=15，求BD=（ ）
| A、16 | ||
| B、20 | ||
C、
| ||
D、
|
