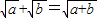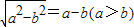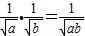题目内容
下列等式中，能成立的有（ ）
①a2m=（a2）m；②a2m=（-am）2；③a2m=（am）2；④a2m=（-a2）m．
①a2m=（a2）m；②a2m=（-am）2；③a2m=（am）2；④a2m=（-a2）m．
分析：根据幂的乘方法则：底数不变，指数相乘，积的乘方法则：把每一个因式分别乘方，再把所得的幂相乘，进行各项的判断即可．
解答：解：①a2m=（a2）m，正确；
②a2m=（-am）2，正确；
③a2m=（am）2正确；
④a2m不一定等于（-a2）m．，当m为偶数时成立，当m为奇数时不成立．
综上可得①②③正确，共3个．
故选B．
②a2m=（-am）2，正确；
③a2m=（am）2正确；
④a2m不一定等于（-a2）m．，当m为偶数时成立，当m为奇数时不成立．
综上可得①②③正确，共3个．
故选B．
点评：本题考查了幂的乘方与积的乘方运算，熟练掌握幂的乘方及积的乘方法则是解答本题的关键．
练习册系列答案
阅读快车系列答案
相关题目
下列等式中，能成立的是（ ）
A、
| ||||||||||||
B、
| ||||||||||||
C、
| ||||||||||||
D、
|
