题目内容
（2006•宿迁）下列计算正确的是（ ）A．a2•a3=a5
B．（a2）3=a5
C．a10÷a2=a5
D．2a5-a5=2
【答案】分析：根据同底数幂相乘，底数不变指数相加；幂的乘方，底数不变指数相乘；同底数幂相除，底数不变指数相减；合并同类项法则，只把系数相加减，字母与字母的次数不变，对各选项分析判断后利用排除法求解．
解答：解：A、a2•a3=a5，正确；
B、应为（a2）3=a6，故本选项错误；
C、应为a10÷a2=a8，故本选项错误；
D、应为2a5-a5=a5，故本选项错误．
故选A．
点评：本题考查同底数幂的乘法，幂的乘方的性质，同底数幂的除法，合并同类项法则，熟练掌握运算性质是解题的关键．
解答：解：A、a2•a3=a5，正确；
B、应为（a2）3=a6，故本选项错误；
C、应为a10÷a2=a8，故本选项错误；
D、应为2a5-a5=a5，故本选项错误．
故选A．
点评：本题考查同底数幂的乘法，幂的乘方的性质，同底数幂的除法，合并同类项法则，熟练掌握运算性质是解题的关键．
练习册系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
（2006•宿迁）设边长为2a的正方形的中心A在直线l上，它的一组对边垂直于直线l，半径为r的⊙O的圆心O在直线l上运动，点A、O间距离为d．
（1）如图①，当r＜a时，根据d与a、r之间关系，将⊙O与正方形的公共点个数填入下表：
所以，当r＜a时，⊙O与正方形的公共点的个数可能有______个；
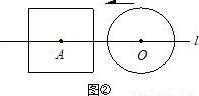
（2）如图②，当r=a时，根据d与a、r之间关系，将⊙O与正方形的公共点个数填入下表：
所以，当r=a时，⊙O与正方形的公共点个数可能有______个；
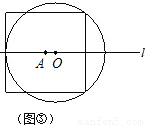
（3）如图③，当⊙O与正方形有5个公共点时，试说明r=
a；
（4）就r＞a的情形，请你仿照“当…时，⊙O与正方形的公共点个数可能有______个”的形式，至少给出一个关于“⊙O与正方形的公共点个数”的正确结论．
（注：第（4）小题若多给出一个正确结论，则可多得2分，但本大题得分总和不得超过12分）．
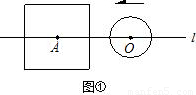
（1）如图①，当r＜a时，根据d与a、r之间关系，将⊙O与正方形的公共点个数填入下表：
| d、a、r之间关系 | 公共点的个数 |
| d＞a+r | |
d=a+r | |
| a≤d＜a+r | |
| d=a-r | |
| d＜a-r |
（2）如图②，当r=a时，根据d与a、r之间关系，将⊙O与正方形的公共点个数填入下表：
| d、a、r之间关系 | 公共点的个数 |
| d＞a+r | |
| d=a+r | |
| a≤d＜a+r | |
| d＜a |
（3）如图③，当⊙O与正方形有5个公共点时，试说明r=
a；（4）就r＞a的情形，请你仿照“当…时，⊙O与正方形的公共点个数可能有______个”的形式，至少给出一个关于“⊙O与正方形的公共点个数”的正确结论．
（注：第（4）小题若多给出一个正确结论，则可多得2分，但本大题得分总和不得超过12分）．