题目内容
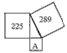
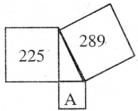 4、如下图以直角三角形三条边为边分别向外作三个正方形,其中两个正方形的面积分别为225和289,则图中正方形字母A所代表的正方形的面积为( )
4、如下图以直角三角形三条边为边分别向外作三个正方形,其中两个正方形的面积分别为225和289,则图中正方形字母A所代表的正方形的面积为( )分析:根据正方形的面积等于边长的平方,由正方形PQED的面积和正方形PRQF的面积分别表示出PR的平方及PQ的平方,又三角形PQR为直角三角形,根据勾股定理求出QR的平方,即为所求正方形的面积.
解答:
解:∵正方形PQED的面积等于225,
∴即PQ2=225,
∵正方形PRGF的面积为289,
∴PR2=289,
又△PQR为直角三角形,根据勾股定理得:
PR2=PQ2+QR2,
∴QR2=PR2-PQ2=289-225=64,
则正方形QMNR的面积为64.
故选D.

解:∵正方形PQED的面积等于225,
∴即PQ2=225,
∵正方形PRGF的面积为289,
∴PR2=289,
又△PQR为直角三角形,根据勾股定理得:
PR2=PQ2+QR2,
∴QR2=PR2-PQ2=289-225=64,
则正方形QMNR的面积为64.
故选D.
点评:此题考查了勾股定理,以及正方形的面积公式.勾股定理最大的贡献就是沟通“数”与“形”的关系,它的验证和利用都体现了数形结合的思想,即把图形的性质问题转化为数量关系的问题来解决.能否由实际的问题,联想到用勾股定理的知识来求解是本题的关键.

练习册系列答案
相关题目


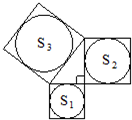 5、如下图,分别以直角三角形的三边为边长向外作正方形,然后分别以三个正方形的中心为圆心,正方形边长的一半为半径作圆,记三个圆的面积分别为S1,S2,S3,则S1,S2,S3之间的关系是( )
5、如下图,分别以直角三角形的三边为边长向外作正方形,然后分别以三个正方形的中心为圆心,正方形边长的一半为半径作圆,记三个圆的面积分别为S1,S2,S3,则S1,S2,S3之间的关系是( )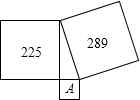 如下图以直角三角形三条边为边分别向外作三个正方形,其中两个正方形的面积分别为225和289,则图中正方形字母A所代表的正方形的面积为
如下图以直角三角形三条边为边分别向外作三个正方形,其中两个正方形的面积分别为225和289,则图中正方形字母A所代表的正方形的面积为