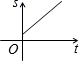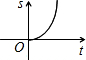题目内容
一个小球在一个斜坡上由静止开始向下运动,通过仪器观察得到小球滚动的距离s(米)与时间t(秒)的数据如下表:
| 时间t | 1 | 2 | 3 | 4 | … |
| 距离s | 2 | 8 | 18 | 32 | … |
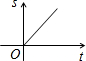
- A.

- B.
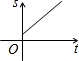
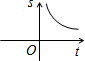
- C.
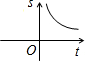
- D.
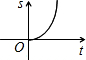
D
分析:通过观察发现:距离都为偶数,应都与2有关,所以表中数据的规律可以确定为t秒时,距离为2×t2.据此可以判定函数图象为抛物线,从而得到答案.
解答:∵1秒时,距离为2;
2秒时,距离为2×4=2×22;
3秒时,距离为2×9=2×32;
4秒时,距离为2×16=2×42;
∴t秒时,距离为2×t2 s=2t2.
∴函数解析式为s=2t2(t≥0).
故选D.
点评:本题考查了二次函数的应用题.解决本题的关键是发现距离都与2有关,进而得到规律.
分析:通过观察发现:距离都为偶数,应都与2有关,所以表中数据的规律可以确定为t秒时,距离为2×t2.据此可以判定函数图象为抛物线,从而得到答案.
解答:∵1秒时,距离为2;
2秒时,距离为2×4=2×22;
3秒时,距离为2×9=2×32;
4秒时,距离为2×16=2×42;
∴t秒时,距离为2×t2 s=2t2.
∴函数解析式为s=2t2(t≥0).
故选D.
点评:本题考查了二次函数的应用题.解决本题的关键是发现距离都与2有关,进而得到规律.

练习册系列答案
相关题目
一个小球在一个斜坡上由静止开始向下运动,通过仪器观察得到小球滚动的距离s(米)与时间t(秒)的数据如下表:
|
一个小球在一个斜坡上由静止开始向下运动,通过仪器观察得到小球滚动的距离s(米)与时间t(秒)的数据如下表:
则距离s与时间t的函数关系图象可能是( )
A.
B.
C.
D.
| 时间t | 1 | 2 | 3 | 4 | … |
| 距离s | 2 | 8 | 18 | 32 | … |
A.

B.

C.

D.