题目内容
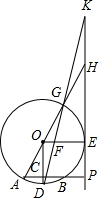 (2012•上城区二模)如图,⊙O的半径OD经过弦AB(不是直径)的中点C,OE∥AB交⊙O于点E,PE∥OD,延长直径AG,交PE于点H,直线DG交OE于点F,交PE于K.若EF=2,FO=1,则KH的长度等于
(2012•上城区二模)如图,⊙O的半径OD经过弦AB(不是直径)的中点C,OE∥AB交⊙O于点E,PE∥OD,延长直径AG,交PE于点H,直线DG交OE于点F,交PE于K.若EF=2,FO=1,则KH的长度等于2
2
.分析:根据△OFD∽△EFK,可将KE的长求出,由OG=OD,可知∠OGD=∠ODG,根据PE∥OD,可知∠K=∠ODG,因为对顶角∠OGD=∠HGK,可得∠K=∠HGK,故HK=HG,进而利用勾股定理得出即可.
解答: 解:∵EF=2,OF=1,
解:∵EF=2,OF=1,
∴EO=DO=3,
∵PE∥OD,
∴∠KEO=∠DOE,∠K=∠ODG,
∴△OFD∽△EFK,
∴EF:OF=KE:OD=2:1
∴KE=6,
∵AC=BC,AB不是直径,
∴OD⊥AB,∠PCO=90°,
∵PE∥OD,
∴∠P=90°,
∵EO∥AB,
∴∠PEO=90°,
∵OG=OD,
∴∠OGD=∠ODG,
∵PE∥OD,
∴∠K=∠ODG,
∵∠OGD=∠HGK,
∴∠K=∠HGK,
∴HK=HG,
设KH=HG=x,
则HE=6-x,HO=3+x,EO=3,
则EO2+HE2=HO2,
即32+(6-x)2=(3+x)2,
解得:x=2,
故KH的长度等于2,
故答案为:2.
 解:∵EF=2,OF=1,
解:∵EF=2,OF=1,∴EO=DO=3,
∵PE∥OD,
∴∠KEO=∠DOE,∠K=∠ODG,
∴△OFD∽△EFK,
∴EF:OF=KE:OD=2:1
∴KE=6,
∵AC=BC,AB不是直径,
∴OD⊥AB,∠PCO=90°,
∵PE∥OD,
∴∠P=90°,
∵EO∥AB,
∴∠PEO=90°,
∵OG=OD,
∴∠OGD=∠ODG,
∵PE∥OD,
∴∠K=∠ODG,
∵∠OGD=∠HGK,
∴∠K=∠HGK,
∴HK=HG,
设KH=HG=x,
则HE=6-x,HO=3+x,EO=3,
则EO2+HE2=HO2,
即32+(6-x)2=(3+x)2,
解得:x=2,
故KH的长度等于2,
故答案为:2.
点评:本题考查了三角形相似的判定和应用以及垂径定理、勾股定理等知识应用,根据已知利用三角形相似得出KE长度,进而得出HK=HG是解题关键.

练习册系列答案
相关题目
 (2012•上城区二模)如图,AB∥CD,EF⊥AB于E,EF交CD于F,已知∠1=63°,则∠2=( )
(2012•上城区二模)如图,AB∥CD,EF⊥AB于E,EF交CD于F,已知∠1=63°,则∠2=( )