Question

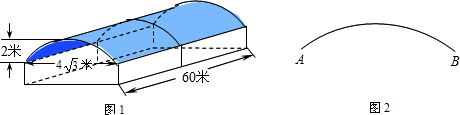
图1是某学校存放学生自行车的车棚的示意图（尺寸如图所示），车棚顶部是圆柱侧面的一部分，其展开图是矩形．图2是车棚顶部截面的示意图，所在圆的圆心为O．车棚顶部是用一种帆布覆盖的，求覆盖棚顶的帆布的面积．（不考虑接缝等因素，计算结果保留π）

Answer 1

【答案】分析：根据题意，由圆的基本性质，可通过作辅助线建立模形，利用垂径定理解答，也可用相交弦定理来解．
解答：解：连接OB，过点O作OE⊥AB，垂足为E，交于F，如图，
由垂径定理，可知：E是AB中点，F是中点，
∴EF是弓形高，
∴AE=AB=2，EF=2，
设半径为R米，则OE=（R-2）米，
在Rt△AOE中，由勾股定理，得R²=（R-2）²+（2）²，
解得R=4，
∵sin∠AOE=，
∴∠AOE=60°，
∴∠AOB=120度．
∴的长为=π（m），
∴帆布的面积为π×60=160π（平方米）．
点评：本题考查用方程解几何问题，方程是解决几何有关计算问题的有效的方法和工具，通常结合勾股定理的形式出现．
部分学生遇此问题，不能将实际问题抽象为数学问题．突破方法：联系实际，将车棚顶部展开得长方形，其长为车棚长，宽为弧AB长．解题关键：在利用数学知识解决实际问题时，要善于把实际问题与数学中的理论知识联系起来，能将生活中的问题抽象为数学问题．