题目内容
【题目】如果方程x2+px+q=0有两个实数根x1 , x2 , 那么x1+x2=﹣p,x1x2=q,请根据以上结论,解决下列问题:
(1)已知a、b是方程x2+15x+5=0的二根,则![]() =?
=?
(2)已知a、b、c满足a+b+c=0,abc=16,求正数c的最小值.
(3)结合二元一次方程组的相关知识,解决问题:已知![]() 和
和![]() 是关于x,y的方程组
是关于x,y的方程组![]() 的两个不相等的实数解.问:是否存在实数k,使得y1y2﹣
的两个不相等的实数解.问:是否存在实数k,使得y1y2﹣![]() =2?若存在,求出的k值,若不存在,请说明理由.
=2?若存在,求出的k值,若不存在,请说明理由.
【答案】解:(1)∵a、b是方程x2+15x+5=0的二根,
∴a+b=﹣15,ab=5,
∴![]() =
=![]() =
=![]() =43,
=43,
故答案是:43;
(2)∵a+b+c=0,abc=16,
∴a+b=﹣c,ab=![]() ,
,
∴a、b是方程x2+cx+![]() =0的解,
=0的解,
∴c2﹣4![]() ≥0,c2﹣
≥0,c2﹣![]() ≥0,
≥0,
∵c是正数,
∴c3﹣43≥0,c3≥43 , c≥4,
∴正数c的最小值是4.
(3)存在,当k=﹣2时,![]() .
.
由x2﹣y+k=0变形得:y=x2+k,
由x﹣y=1变形得:y=x﹣1,把y=x﹣1代入y=x2+k,并整理得:x2﹣x+k+1=0,
由题意思可知,x1 , x2是方程x2﹣x+k+1=0的两个不相等的实数根,故有: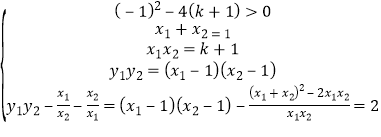
即:
解得:k=﹣2.
【解析】(1)根据a,b是x2+15x+5=0的解,求出a+b和ab的值,即可求出![]() 的值.
的值.
(2)根据a+b+c=0,abc=16,得出a+b=﹣c,ab=![]() , a、b是方程x2+cx+
, a、b是方程x2+cx+![]() =0的解,再根据c2﹣4
=0的解,再根据c2﹣4![]() ≥0,即可求出c的最小值.
≥0,即可求出c的最小值.
(3)运用根与系数的关系求出x1+x2=1,x1x2=k+1,再解y1y2﹣![]() =2,即可求出k的值.
=2,即可求出k的值.
【考点精析】解答此题的关键在于理解求根公式的相关知识,掌握根的判别式△=b2-4ac,这里可以分为3种情况:1、当△>0时,一元二次方程有2个不相等的实数根2、当△=0时,一元二次方程有2个相同的实数根3、当△<0时,一元二次方程没有实数根,以及对根与系数的关系的理解,了解一元二次方程ax2+bx+c=0(a≠0)的根由方程的系数a、b、c而定;两根之和等于方程的一次项系数除以二次项系数所得的商的相反数;两根之积等于常数项除以二次项系数所得的商.

【题目】国务院办公厅2015年3月16日发布了《中国足球改革的总体方案》,这是中国足球历史上的重大改革.为了进一步普及足球知识,传播足球文化,我市举行了“足球进校园”知识竞赛活动,为了解足球知识的普及情况,随机抽取了部分获奖情况进行整理,得到下列不完整的统计图表:
获奖等次 | 频数 | 频率 |
一等奖 | 10 | 0.05 |
二等奖 | 20 | 0.10 |
三等奖 | 30 | b |
优胜奖 | a | 0.30 |
鼓励奖 | 80 | 0.40 |
请根据所给信息,解答下列问题:
(1)a= ,b= ,且补全频数分布直方图;
(2)若用扇形统计图来描述获奖分布情况,问获得优胜奖对应的扇形圆心角的度数是多少?
(3)在这次竞赛中,甲、乙、丙、丁四位同学都获得一等奖,若从这四位同学中随机选取两位同学代表我市参加上一级竞赛,请用树状图或列表的方法,计算恰好选中甲、乙二人的概率.

【题目】小明学完了统计知识后,从“中国环境保护网”上查询到他所居住城市2009年全年的空气质量级别资料,用简单随机抽样的方法选取30天,并列出下表:
空气质量级别 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 |
天数 | a | 15 | 2 | 1 | 0 |
请你根据以上信息解答下面问题:
(1)这次抽样中“空气质量不低于良”的频率为多少?
(2)根据这次抽样的结果,请你估计2009年全年(共365天)空气质量为优的天数是多少?
