题目内容
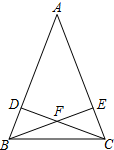
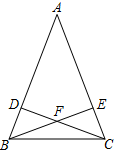 如图,AB和AC是等腰△ABC的两腰,CD和BE是两腰上的高,CD和BE相交于点F.
如图,AB和AC是等腰△ABC的两腰,CD和BE是两腰上的高,CD和BE相交于点F.
(1)在不增加辅助线的前提下,这个图形中共有哪几对全等三角形?请一一写出.
(2)请你在(1)的结论中选择一个说明理由.
解:(1)△ABE≌△ACD;△DBC≌△ECB;△DFB≌△EFC;
(2)△ABE≌△ACD,
理由如下:
∵CD和BE是两腰上的高,
∴∠AEB=∠ADC=90°,
在△ABE和△ACD中,
∵ ,
,
∴△ABE≌△ACD(AAS).
分析:(1)根据△ABC是等腰三角形可得∠ABC=∠ACB,AB=AC,再有CD和BE是两腰上的高,可得∠AEB=∠ADC=90°,进而可判断出△ABE≌△ACD;△DBC≌△ECB;△DFB≌△EFC;
(2)证明△ABE≌△ACD,根据条件可得∠AEB=∠ADC=90°,再有条件∠A=∠A,AB=AC可利用AAS判定两个三角形全等.
点评:此题主要考查了三角形全等的判定,关键是掌握判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.
注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.
(2)△ABE≌△ACD,
理由如下:
∵CD和BE是两腰上的高,
∴∠AEB=∠ADC=90°,
在△ABE和△ACD中,
∵
 ,
,∴△ABE≌△ACD(AAS).
分析:(1)根据△ABC是等腰三角形可得∠ABC=∠ACB,AB=AC,再有CD和BE是两腰上的高,可得∠AEB=∠ADC=90°,进而可判断出△ABE≌△ACD;△DBC≌△ECB;△DFB≌△EFC;
(2)证明△ABE≌△ACD,根据条件可得∠AEB=∠ADC=90°,再有条件∠A=∠A,AB=AC可利用AAS判定两个三角形全等.
点评:此题主要考查了三角形全等的判定,关键是掌握判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.
注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
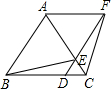 F=AE,连接AF、BE和CF.
F=AE,连接AF、BE和CF.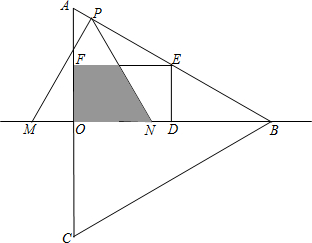 边在△AOB内部作如图所示的矩形ODEF,点E在线段AB上.
边在△AOB内部作如图所示的矩形ODEF,点E在线段AB上.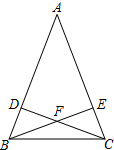 如图,AB和AC是等腰△ABC的两腰,CD和BE是两腰上的高,CD和BE相交于点F.
如图,AB和AC是等腰△ABC的两腰,CD和BE是两腰上的高,CD和BE相交于点F.