Question

已知一等腰梯形，则连接它各边中点所得到的四边形为（　　）

A．矩形

B．平行四边形

C．菱形

D．正方形

Answer 1

分析：连接AC、BD，可证MN为△ABD的中位线，PQ为△CBD的中位线，根据中位线定理可证MN∥BD∥PQ，MN=PQ=

1

2

BD，同理可证PN∥AC∥MQ，NP=MQ=

1

2

AC，根据等腰梯形的性质可知AC=BD，故可证四边形PQMN为菱形．

解答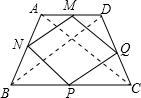：解：连接AC、BD，
∵M、N分别为AD、AB的中点
∴MN为△ABD的中位线，∴MN∥BD，MN=

1

2

BD，
同理可证BD∥PQ，PQ=

1

2

BD，
∴MN=PQ，MN∥PQ，四边形PQMN为平行四边形，
同理可证NP=MQ=

1

2

AC，
根据等腰梯形的性质可知AC=BD，
∴PQ=NP，
∴?PQMN为菱形．
故选C．

点评：本题主要考查等腰梯形的性质在证明特殊平行四边形中的应用．同时运用了三角形的中位线定理．