题目内容
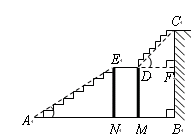
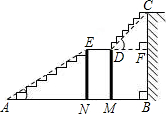 如图是某宾馆大厅到二楼的楼梯设计图,已知BC=6米,AB=9米,中间平台宽度DE为2米,DM,EN为平台的两根支柱,DM,EN垂直于AB,垂足分别为M,N,∠EAB=30°,∠CDF=45°.求DM和BC的水平距离BM.(精确到0.1米,参考数据:
如图是某宾馆大厅到二楼的楼梯设计图,已知BC=6米,AB=9米,中间平台宽度DE为2米,DM,EN为平台的两根支柱,DM,EN垂直于AB,垂足分别为M,N,∠EAB=30°,∠CDF=45°.求DM和BC的水平距离BM.(精确到0.1米,参考数据:| 2 |
| 3 |
分析:设DF=x米.由等腰直角三角形的性质知,CF=DF=x,得EN=FB=BC-CF=6-x,AN=AB-DF-ED=7-x,则在直角三角形ANE中,有EN=AN•tan30°,建立方程求得x的值.
解答:解:设DF=x米.
∵∠CDF=45°,∠CFD=90°,
∴CF=DF=x米,
∴BF=BC-CF=(6-x)米.
∴EN=DM=BF=(6-x)米.
∵AB=9米,DE=2米,BM=DF=x米,
∴AN=AB-MN-BM=(7-x)米.
在△AEN中,∠ANE=90°,∠EAN=30°,
∴EN=AN•tan30°.
即6-x=
(7-x).
解这个方程得:x=
≈4.6.
答:支柱DM距BC的水平距离约为4.6米.
∵∠CDF=45°,∠CFD=90°,
∴CF=DF=x米,
∴BF=BC-CF=(6-x)米.
∴EN=DM=BF=(6-x)米.
∵AB=9米,DE=2米,BM=DF=x米,
∴AN=AB-MN-BM=(7-x)米.
在△AEN中,∠ANE=90°,∠EAN=30°,
∴EN=AN•tan30°.
即6-x=
| ||
| 3 |
解这个方程得:x=
18-7
| ||
3-
|
答:支柱DM距BC的水平距离约为4.6米.
点评:本题通过设适当的参数,利用直角三角形的边角关系建立方程而求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
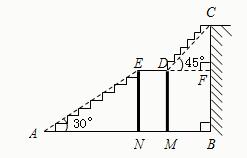 9、如图是某宾馆大厅到二楼的楼梯截面图,已知BC=6米,AB=9米,中间平台DE与地面AB平行,且DE的长度为2米,DM、EN为平台的两根支柱,DM、EN垂直于AB,垂足分别为M、N,∠EAB=30°,∠CDF=45°,楼梯宽度为3米.
9、如图是某宾馆大厅到二楼的楼梯截面图,已知BC=6米,AB=9米,中间平台DE与地面AB平行,且DE的长度为2米,DM、EN为平台的两根支柱,DM、EN垂直于AB,垂足分别为M、N,∠EAB=30°,∠CDF=45°,楼梯宽度为3米.
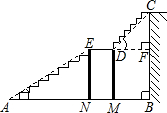 如图是某宾馆大厅到二楼的楼梯设计图,已知BC=6米,AB=9米,中间平台宽度DE为2米,DM,EN为平台的两根支柱,且DM,EN均垂直于AB,垂足分别为M,N,∠EAB=30°,∠CDF=45°.则求BM的长度.(精确到0.1米)
如图是某宾馆大厅到二楼的楼梯设计图,已知BC=6米,AB=9米,中间平台宽度DE为2米,DM,EN为平台的两根支柱,且DM,EN均垂直于AB,垂足分别为M,N,∠EAB=30°,∠CDF=45°.则求BM的长度.(精确到0.1米)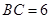 米,
米,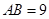 米,中间平台宽度
米,中间平台宽度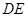 为2米,
为2米,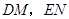 为平台的两根支柱,
为平台的两根支柱,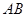 ,垂足分别为
,垂足分别为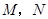 ,
,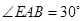 ,
,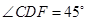 .求
.求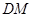 和
和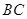 的水平距离
的水平距离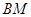 .(精确到0.1米,参考数据:
.(精确到0.1米,参考数据: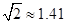 ,
,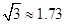 )
)