题目内容
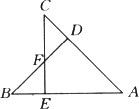
如图,如果AB=AC,BD⊥AC于D,CE⊥AB于E,BD、CE相交于点F,那么BE和CD相等吗?说明理由.
答案:
解析:
解析:
|
思路分析:按常规说明BE与CD相等,可说明它们所在的三角形全等,即△BEF和△CDF,由条件可知,在△BEF和△CDF中,仅有对顶角相等及∠BEF=∠CDF=90°两个条件,缺少一边,故此路不通,这需另辟蹊径.进一步观察图形,若能说明AD=AE,则由AB=AC,可说明BE=CD.AD与AE分别在△ABD和△ACE中,由已知条件可说明这两个三角形全等,此路畅通. 课标剖析:当不能直接说明两线段(或角)所在的三角形全等,从而得到线段(或角)相等时,利用证相等线段(或角)的差或和所在的三角形全等来得到结论.是通常的思考方法之一. |

练习册系列答案
相关题目