题目内容
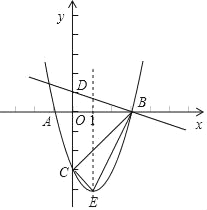
【题目】如图,抛物线y=ax2+bx﹣3(a≠0)的顶点为E,该抛物线与x轴交于A(﹣1,0)、B(3,0)两点,与y轴交于点C,直线y=﹣![]() x+1与y轴交于点D.
x+1与y轴交于点D.
(1)求抛物线的解析式;
(2)证明:△DBO∽△EBC;
(3)在抛物线的对称轴上是否存在点P,使△PBC是等腰三角形?若存在,请直接写出符合条件的P点坐标;若不存在,请说明理由.
【答案】(1)抛物线解析式为y=x2﹣2x﹣3;(2)见解析;(3)存在,P点坐标为(1,﹣1)或P(1, ![]() )或(1,﹣
)或(1,﹣![]() )或(1,﹣3+
)或(1,﹣3+![]() )或(1,﹣3﹣
)或(1,﹣3﹣![]() )时,△PBC是等腰三角形.理由:见解析
)时,△PBC是等腰三角形.理由:见解析
【解析】试题分析:(1)设交点式y=a(x+1)(x-3),则-3a=-3,然后求出a得到抛物线解析式;
(2)先把抛物线解析式配成顶点式得到E(1,-4),再利用一次函数解析式确定D(0,1),则利用两点间的距离公式可计算出BC=3![]() ,BE=2
,BE=2![]() ,CE=
,CE=![]() ,BD=
,BD=![]() ,从而得到
,从而得到![]() ,然后根据相似三角形的判定方法可判断△BCE∽△BDO;
,然后根据相似三角形的判定方法可判断△BCE∽△BDO;
(3)设P(1,m),则利用两点间的距离公式可得BC2=18,PB2=m2+4,PC2=(m+3)2+1,然后讨论:当PB=PC时,△PBC是等腰三角形,则m2+4=(m+3)2+1;当PB=BC时,△PBC是等腰三角形,则m2+4=18;当PC=BC时,△PBC是等腰三角形,则(m+3)2+1=18,接着分别解关于m的方程求出m,从而得到满足条件的P点坐标.
试题解析:(1)解:抛物线的解析式为y=a(x+1)(x-3),
即y=ax2-2ax-3a,
∴-3a=-3,解得a=1,
∴抛物线解析式为y=x2-2x-3;
(2)证明:∵y=x2-2x-3=(x-1)2-4,
∴E(1,-4),
当x=0时,y=-![]() x+1=1,则D(0,1),
x+1=1,则D(0,1),
∵B(3,0),A(-1,0),C(0,-3),
∴BC=![]() ,BE=
,BE=![]() ,CE=
,CE=![]() ,BD=
,BD=![]() ,
,
∵![]() ,
, ![]() ,
, ![]() ,
,
∴![]() ,
,
∴△BCE∽△BDO;
(3)存在,
理由:抛物线的对称轴为直线x=1,设P(1,m),则BC2=18,PB2=(1-3)2+m2=m2+4,PC2=(m+3)2+1,
当PB=PC时,△PBC是等腰三角形,则m2+4=(m+3)2+1,解得m=-1,此时P(1,-1),
当PB=BC时,△PBC是等腰三角形,则m2+4=18,解得m=±![]() ,此时P(1,
,此时P(1, ![]() )或(1,-
)或(1,-![]() )
)
当PC=BC时,△PBC是等腰三角形,则(m+3)2+1=18,解得m=-3±![]() ,此时P(1,-3+
,此时P(1,-3+![]() )或(-3-
)或(-3-![]() ),
),
综上所述,P点坐标为(1,﹣1)或P(1, ![]() )或(1,﹣
)或(1,﹣![]() )或(1,﹣3+
)或(1,﹣3+![]() )或(1,﹣3﹣
)或(1,﹣3﹣![]() )时,△PBC是等腰三角形.
)时,△PBC是等腰三角形.

【题目】观察图形,解答问题:

(1)按下表已填写的形式填写表中的空格:
图① | 图② | 图③ | |
三个角上三个数的积 | 1×(﹣1)×2=﹣2 | (﹣3)×(﹣4)×(﹣5)=﹣60 | |
三个角上三个数的和 | 1+(﹣1)+2=2 | (﹣3)+(﹣4)+(﹣5)=﹣12 | |
积与和的商 | ﹣2÷2=﹣1, |
(2)请用你发现的规律求出图④中的数y和图⑤中的数x.





