题目内容
如果△ABC中，∠A：∠B：∠C=1：2：3，那么BC：AC：AB的值是（ ）
| A、1：2：3 | ||
| B、3：2：1 | ||
C、1：
| ||
D、1：2：
|
分析：根据三角形的内角和求得三角的度数，可得此三角形是直角三角形；再根据特殊角的函数值解直角三角形，求三边的比值．
解答：解：设三个内角的度数分别为∠A=k°，∠B=2k°，∠C=3k°．
根据三角形内角和定理，可知k°+2k°+3k°=180°，得k°=30°
所以∠A=30°，∠B=60°，∠C=90°，
再设BC=X，则AB=
=
=
=2X，AC=BCcot30°=
X，
∴BC：AC：AB=1：
：2．
故选C．
根据三角形内角和定理，可知k°+2k°+3k°=180°，得k°=30°
所以∠A=30°，∠B=60°，∠C=90°，
再设BC=X，则AB=
| BC |
| sinA |
| BC |
| sin30° |
| BC | ||
|
| 3 |
∴BC：AC：AB=1：
| 3 |
故选C．
点评：本题利用了锐角三角函数的概念和三角形内角和定理列方程求解算．
练习册系列答案
相关题目
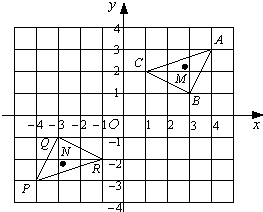15、如图，△PQR是△ABC经过某种变换后得到的图形．如果△ABC中任意一点M的坐标为（a，b），那么它的对应点N的坐标为