Question

如图，从一个半径为1的圆形铁皮中剪下一个圆心角为90°的扇形BAC．
（1）求这个扇形的面积；
（2）若将扇形BAC围成一个圆锥的侧面，这个圆锥的底面直径是多少？能否从最大的余料③中剪出一个圆做该圆锥的底面？请说明理由．

Answer 1

分析：（1）由勾股定理求扇形的半径，再根据面积公式求值；
（2）利用底面周长等于展开图的弧长，可求得直径的长度，进而比较圆锥的底面半径和图中EF的大小关系即可．

解答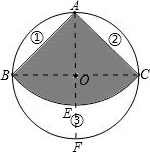：解：（1）∵∠A为直角，
∴直径BC=2，
∴根据勾股定理得：AB²+AC²=BC²，
∵AB=AC，
∴AB²+AB²=2²，
∴扇形半径为AB=

2

；
∴S_扇形=

90π( 2 )2

360

=

π

2

；
（2）设围成圆锥的底面半径为r，则2πr=

90π• 2

180

，解得2r=

2

2

；
延长AO分别交弧BC和⊙O于E、F，而EF=2-

2

＜

2

2

；
∴不能从最大的余料③中剪出一个圆做该圆锥的底面．

点评：此题主要考查了扇形的面积公式和弧长公式及圆锥的展开图等知识．