题目内容
某班参加校运动会的19名运动员的运动服号码恰是1～19号，这些运动员随意地站成一个圆圈，则一定有顺次相邻的某3名运动员，他们运动服号码数之和不小于32，请你说明理由．
见解析
解：设在圆周上按逆时针顺序以1号为起点记运动服号码数为a1，a2，a3，…，a18，a19，
显然a1=1，而a2，a3，…，a18，a19就是2，3，4，5，6，…，18，19的一个排列．
令A1=a2+a3+a4；
A2=a5+a6+a7；
A3=a8+a9+a10；
A4=a11+a12+a13；
A5=a14+a15+a16；
A6=a17+a18+a19；
则A1+A2+A3+A4+A5+A6=a2+a3+a4+…+a17+a18+a19=2+3+4+…+17+18+19=189（*）．
如果A1，A2，A3，A4，A5，A6中每一个都≤31，则有A1+A2+A3+A4+A5+A6≤6×31=186，与（*）式矛盾．
所以A1，A2，A3，A4，A5，A6中至少有一个大于31．为确定起见，不妨就是A1＞31，即a2+a3+a4＞31，但a2+a3+a4是整数，
所以必有a2+a3+a4≥32成立．
所以，一定有顺次相邻的某三名运动员，他们运动服号码数之和不小于32．
由已知，1～19号运动员随意地站成一个圆圈，求出6组有顺次相邻的某3名运动员的号码的和，从每组都小于等于31，得6组的和与计算出6组的和矛盾确定一定有顺次相邻的某三名运动员，他们运动服号码数之和不小于32．
显然a1=1，而a2，a3，…，a18，a19就是2，3，4，5，6，…，18，19的一个排列．
令A1=a2+a3+a4；
A2=a5+a6+a7；
A3=a8+a9+a10；
A4=a11+a12+a13；
A5=a14+a15+a16；
A6=a17+a18+a19；
则A1+A2+A3+A4+A5+A6=a2+a3+a4+…+a17+a18+a19=2+3+4+…+17+18+19=189（*）．
如果A1，A2，A3，A4，A5，A6中每一个都≤31，则有A1+A2+A3+A4+A5+A6≤6×31=186，与（*）式矛盾．
所以A1，A2，A3，A4，A5，A6中至少有一个大于31．为确定起见，不妨就是A1＞31，即a2+a3+a4＞31，但a2+a3+a4是整数，
所以必有a2+a3+a4≥32成立．
所以，一定有顺次相邻的某三名运动员，他们运动服号码数之和不小于32．
由已知，1～19号运动员随意地站成一个圆圈，求出6组有顺次相邻的某3名运动员的号码的和，从每组都小于等于31，得6组的和与计算出6组的和矛盾确定一定有顺次相邻的某三名运动员，他们运动服号码数之和不小于32．
练习册系列答案
相关题目
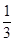
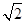，若点B关于A点的对称点为点C，则点C所对应的实数为（ ）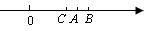
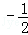的相反数是（ ）