题目内容
(1999•成都)已知直线y= x和y=-x+m,二次函数y=x2+px+q的图象的顶点为M.
x和y=-x+m,二次函数y=x2+px+q的图象的顶点为M.(1)若M恰好在直线y=
 x与y=-x+m的交点处,试证明:无论m取何实数值,二次函数y=x2+px+q的图象与直线y=-x+m总有两个不同的交点.
x与y=-x+m的交点处,试证明:无论m取何实数值,二次函数y=x2+px+q的图象与直线y=-x+m总有两个不同的交点.(2)在(1)的条件下,若直线y=-x+m过点D(0,-3),求二次函数y=x2+px+q的表达式,并作出其大致图象.
(3)在(2)的条件下,若二次函数y=x2+px+q的图象与y轴交于点C,与x轴的左交点为A,试在直线y=
 x上求异于M的点P,使点P在△CMA的外接圆上.
x上求异于M的点P,使点P在△CMA的外接圆上.
【答案】分析:(1)由直线y= x和y=-x+m相交,解出交点,二次函数y=x2+px+q的图象的顶点为M,M是交点,写出二次函数带有m的函数关系式,再解出根的判别式,可证交点的个数.
x和y=-x+m相交,解出交点,二次函数y=x2+px+q的图象的顶点为M,M是交点,写出二次函数带有m的函数关系式,再解出根的判别式,可证交点的个数.
(2)由直线y=-x+m过点D(0,-3),解出m,即可写出函数关系式,作出图象.
(3)由勾股定理,可知△CMA为Rt△,且∠CMA=90°,MC为△CMA外接圆直径,设过点P(n, n),分别作PN⊥y轴于N,PQ⊥x轴于R,过M作MS⊥y轴于S,MS的延长线与PR的延长线交于点Q.由勾股定理|MP|2=|MQ|2+|QP|2,然后解出n.
n),分别作PN⊥y轴于N,PQ⊥x轴于R,过M作MS⊥y轴于S,MS的延长线与PR的延长线交于点Q.由勾股定理|MP|2=|MQ|2+|QP|2,然后解出n.
解答:(1)证明:由 有
有 =-x+m
=-x+m
∴ ,
, ,
, ,
,
交点( ,
, ),
),
此时二次函数为y=(x- m)2+
m)2+ m=
m= m③
m③
由②、③联立,消去y,有


△=[-( )2]-4(
)2]-4(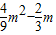 )
)
= m2+
m2+
=1>0
∴无论m为何实数值,二次函数y=x2+px+q的图象与直线y=-x+m总有两个不同的交点.
(2)解:∵直线y=-x+m过点D(0,-3),
∴-3=0+m,
∴m=-3,
∴M(-2,-1),
∴二次函数为y=(x+2)2-1=x2+4x+3
=(x+3)(x+1),
图象如下图:
(3)解:由勾股定理,可知△CMA为Rt△,且∠CMA=90°,
∴MC为△CMA外接圆直径.
∵P在y= x上,可设P(n,
x上,可设P(n, n),
n),
由MC为△CMA外接圆的直径,P在这个圆上,
∴∠CPM=90°,
过点P分别作PN⊥y轴于N,PQ⊥x轴于R,过M作MS⊥y轴于S,
MS的延长线与PR的延长线交于点Q.
由勾股定理,有|MP|2=|MQ|2+|QP|2,
即|MP|2=(n+2)2
|CP|2=|NC|2+|NP|2= ,
,
|CM|2=20
而|MP|2+|CP|2=|CM|2,
∴(n+2)2 +
+ +n2=20,
+n2=20,
即 ,
,
∴5n2+4n-12=0,
(5n-6)(n+2)=0,
∴n1= ,n2=-2,
,n2=-2,
而n2=-2即是M点的横坐标,与题意不合,故舍去,
∴n= ,此时
,此时 ,
,
∴P点坐标为( ,
, ).
).
点评:本题是二次函数的综合习题,考查求函数解析式,勾股定理等知识点,习题比较麻烦.
 x和y=-x+m相交,解出交点,二次函数y=x2+px+q的图象的顶点为M,M是交点,写出二次函数带有m的函数关系式,再解出根的判别式,可证交点的个数.
x和y=-x+m相交,解出交点,二次函数y=x2+px+q的图象的顶点为M,M是交点,写出二次函数带有m的函数关系式,再解出根的判别式,可证交点的个数.(2)由直线y=-x+m过点D(0,-3),解出m,即可写出函数关系式,作出图象.
(3)由勾股定理,可知△CMA为Rt△,且∠CMA=90°,MC为△CMA外接圆直径,设过点P(n,
 n),分别作PN⊥y轴于N,PQ⊥x轴于R,过M作MS⊥y轴于S,MS的延长线与PR的延长线交于点Q.由勾股定理|MP|2=|MQ|2+|QP|2,然后解出n.
n),分别作PN⊥y轴于N,PQ⊥x轴于R,过M作MS⊥y轴于S,MS的延长线与PR的延长线交于点Q.由勾股定理|MP|2=|MQ|2+|QP|2,然后解出n.解答:(1)证明:由
 有
有 =-x+m
=-x+m∴
 ,
, ,
, ,
,交点(
 ,
, ),
),此时二次函数为y=(x-
 m)2+
m)2+ m=
m= m③
m③由②、③联立,消去y,有


△=[-(
 )2]-4(
)2]-4(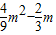 )
)=
 m2+
m2+
=1>0
∴无论m为何实数值,二次函数y=x2+px+q的图象与直线y=-x+m总有两个不同的交点.
(2)解:∵直线y=-x+m过点D(0,-3),

∴-3=0+m,
∴m=-3,
∴M(-2,-1),
∴二次函数为y=(x+2)2-1=x2+4x+3
=(x+3)(x+1),
图象如下图:
(3)解:由勾股定理,可知△CMA为Rt△,且∠CMA=90°,
∴MC为△CMA外接圆直径.
∵P在y=
 x上,可设P(n,
x上,可设P(n, n),
n),由MC为△CMA外接圆的直径,P在这个圆上,
∴∠CPM=90°,
过点P分别作PN⊥y轴于N,PQ⊥x轴于R,过M作MS⊥y轴于S,

MS的延长线与PR的延长线交于点Q.
由勾股定理,有|MP|2=|MQ|2+|QP|2,
即|MP|2=(n+2)2

|CP|2=|NC|2+|NP|2=
 ,
,|CM|2=20
而|MP|2+|CP|2=|CM|2,
∴(n+2)2
 +
+ +n2=20,
+n2=20,即
 ,
,∴5n2+4n-12=0,
(5n-6)(n+2)=0,
∴n1=
 ,n2=-2,
,n2=-2,而n2=-2即是M点的横坐标,与题意不合,故舍去,
∴n=
 ,此时
,此时 ,
,∴P点坐标为(
 ,
, ).
).点评:本题是二次函数的综合习题,考查求函数解析式,勾股定理等知识点,习题比较麻烦.

练习册系列答案
相关题目
 x和y=-x+m,二次函数y=x2+px+q的图象的顶点为M.
x和y=-x+m,二次函数y=x2+px+q的图象的顶点为M. x与y=-x+m的交点处,试证明:无论m取何实数值,二次函数y=x2+px+q的图象与直线y=-x+m总有两个不同的交点.
x与y=-x+m的交点处,试证明:无论m取何实数值,二次函数y=x2+px+q的图象与直线y=-x+m总有两个不同的交点. x上求异于M的点P,使点P在△CMA的外接圆上.
x上求异于M的点P,使点P在△CMA的外接圆上.