题目内容
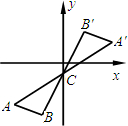 如图,将△ABC 绕点C(0,-1)旋转180°得到△A′B′C,设点A 的坐标为(-4,-3),则点A′的坐标为
如图,将△ABC 绕点C(0,-1)旋转180°得到△A′B′C,设点A 的坐标为(-4,-3),则点A′的坐标为
- A.(5,2)
- B.(4,3)
- C.(4,2)
- D.(4,1)
D
分析:分别过A,A′向y轴引垂线,可得△A′EC≌△ADC,利用全等得到A到x轴,y轴的距离,进而根据所在象限可得相应坐标.
解答: 解:作A′E⊥y轴于点E,AD⊥y轴于点D,则∠A′EC=∠ADC,
解:作A′E⊥y轴于点E,AD⊥y轴于点D,则∠A′EC=∠ADC,
∵∠A′CE=∠ACD,AC=A′C,
∴△A′EC≌△ADC,
∴AD=A′E=4,CE=CD,
∵OD=3,OC=1,
∴CD=2,
∴CE=2,
∴OE=1,
∴点A′的坐标为(4,-1).
故选D.
点评:考查坐标的旋转变换问题;利用全等得到对应点的坐标是解决本题的突破点.
分析:分别过A,A′向y轴引垂线,可得△A′EC≌△ADC,利用全等得到A到x轴,y轴的距离,进而根据所在象限可得相应坐标.
解答:
 解:作A′E⊥y轴于点E,AD⊥y轴于点D,则∠A′EC=∠ADC,
解:作A′E⊥y轴于点E,AD⊥y轴于点D,则∠A′EC=∠ADC,∵∠A′CE=∠ACD,AC=A′C,
∴△A′EC≌△ADC,
∴AD=A′E=4,CE=CD,
∵OD=3,OC=1,
∴CD=2,
∴CE=2,
∴OE=1,
∴点A′的坐标为(4,-1).
故选D.
点评:考查坐标的旋转变换问题;利用全等得到对应点的坐标是解决本题的突破点.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
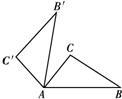 6、如图,将△ABC绕点A逆时针旋转80°得到△AB′C′.若∠BAC=50°,则∠CAB′的度数为( )
6、如图,将△ABC绕点A逆时针旋转80°得到△AB′C′.若∠BAC=50°,则∠CAB′的度数为( ) 如图,将△ABC绕顶点A逆时针旋转一角度,使点D落在BC边上,得到△ADE,此时恰好AB∥DE,已知∠E=35°,求∠DAC的度数.
如图,将△ABC绕顶点A逆时针旋转一角度,使点D落在BC边上,得到△ADE,此时恰好AB∥DE,已知∠E=35°,求∠DAC的度数.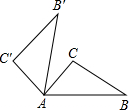 如图,将△ABC绕点A逆时针旋转80°得到△AB′C′.若∠BAC=50°,则∠CAB′的度数为
如图,将△ABC绕点A逆时针旋转80°得到△AB′C′.若∠BAC=50°,则∠CAB′的度数为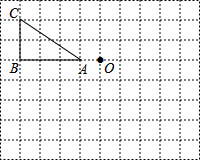 (1)计算:
(1)计算: 如图,将△ABC绕顶点A顺时针旋转60°后得到△AB′C′,且C′为BC的中点.若D为B′C′与AB的交点,则C′D:DB′=
如图,将△ABC绕顶点A顺时针旋转60°后得到△AB′C′,且C′为BC的中点.若D为B′C′与AB的交点,则C′D:DB′=