题目内容
(2010•北京)已知反比例函数y=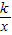 的图象经过点A(-
的图象经过点A(-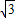 ,1).
,1).(1)试确定此反比例函数的解析式;
(2)点O是坐标原点,将线段OA绕O点顺时针旋转30°得到线段OB.判断点B是否在此反比例函数的图象上,并说明理由;
(3)已知点P(m,
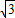 m+6)也在此反比例函数的图象上(其中m<0),过P点作x轴的垂线,交x轴于点M.若线段PM上存在一点Q,使得△OQM的面积是
m+6)也在此反比例函数的图象上(其中m<0),过P点作x轴的垂线,交x轴于点M.若线段PM上存在一点Q,使得△OQM的面积是 ,设Q点的纵坐标为n,求n2-2
,设Q点的纵坐标为n,求n2-2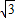 n+9的值.
n+9的值.
【答案】分析:(1)由于反比例函数y=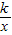 的图象经过点A(-
的图象经过点A(-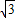 ,1),运用待定系数法即可求出此反比例函数的解析式;
,1),运用待定系数法即可求出此反比例函数的解析式;
(2)首先由点A的坐标,可求出OA的长度,∠AOC的大小,然后根据旋转的性质得出∠AOB=30°,OB=OA,再求出点B的坐标,进而判断点B是否在此反比例函数的图象上;
(3)把点P(m,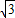 m+6)代入反比例函数的解析式,得到关于m的一元二次方程;根据题意,可得Q点的坐标为(m,n),再由△OQM的面积是
m+6)代入反比例函数的解析式,得到关于m的一元二次方程;根据题意,可得Q点的坐标为(m,n),再由△OQM的面积是 ,根据三角形的面积公式及m<0,得出mn的值,最后将所求的代数式变形,把mn的值代入,即可求出n2-2
,根据三角形的面积公式及m<0,得出mn的值,最后将所求的代数式变形,把mn的值代入,即可求出n2-2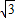 n+9的值.
n+9的值.
解答:解:(1)由题意得1=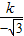 ,解得k=-
,解得k=-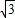 ,
,
∴反比例函数的解析式为y=-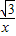 ;
;
(2)过点A作x轴的垂线交x轴于点C.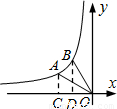
在Rt△AOC中,OC=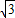 ,AC=1,
,AC=1,
∴OA=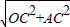 =2,∠AOC=30°,
=2,∠AOC=30°,
∵将线段OA绕O点顺时针旋转30°得到线段OB,
∴∠AOB=30°,OB=OA=2,
∴∠BOC=60°.
过点B作x轴的垂线交x轴于点D.
在Rt△BOD中,BD=OB•sin∠BOD=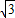 ,OD=
,OD= OB=1,
OB=1,
∴B点坐标为(-1,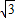 ),
),
将x=-1代入y=-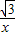 中,得y=
中,得y=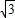 ,
,
∴点B(-1,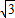 )在反比例函数y=-
)在反比例函数y=-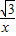 的图象上.
的图象上.
(3)由y=-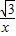 得xy=-
得xy=-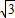 ,
,
∵点P(m,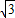 m+6)在反比例函数y=-
m+6)在反比例函数y=-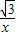 的图象上,其中m<0,
的图象上,其中m<0,
∴m(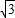 m+6)=-
m+6)=-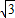 ,
,
∴m2+2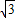 m+1=0,
m+1=0,
∵PQ⊥x轴,∴Q点的坐标为(m,n).
∵△OQM的面积是 ,
,
∴ OM•QM=
OM•QM= ,
,
∵m<0,∴mn=-1,
∴m2n2+2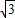 mn2+n2=0,
mn2+n2=0,
∴n2-2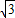 n=-1,
n=-1,
∴n2-2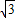 n+9=8.
n+9=8.
点评:本题综合考查了运用待定系数法求反比例函数的解析式,旋转的性质,三角函数的定义,求代数式的值等知识,尤其是在最后一问中,没有必要求出n的具体值,而是将mn=-1作为一个整体代入,有一定的技巧性,使计算简便.
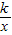 的图象经过点A(-
的图象经过点A(-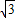 ,1),运用待定系数法即可求出此反比例函数的解析式;
,1),运用待定系数法即可求出此反比例函数的解析式;(2)首先由点A的坐标,可求出OA的长度,∠AOC的大小,然后根据旋转的性质得出∠AOB=30°,OB=OA,再求出点B的坐标,进而判断点B是否在此反比例函数的图象上;
(3)把点P(m,
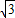 m+6)代入反比例函数的解析式,得到关于m的一元二次方程;根据题意,可得Q点的坐标为(m,n),再由△OQM的面积是
m+6)代入反比例函数的解析式,得到关于m的一元二次方程;根据题意,可得Q点的坐标为(m,n),再由△OQM的面积是 ,根据三角形的面积公式及m<0,得出mn的值,最后将所求的代数式变形,把mn的值代入,即可求出n2-2
,根据三角形的面积公式及m<0,得出mn的值,最后将所求的代数式变形,把mn的值代入,即可求出n2-2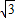 n+9的值.
n+9的值.解答:解:(1)由题意得1=
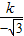 ,解得k=-
,解得k=-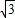 ,
,∴反比例函数的解析式为y=-
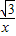 ;
;(2)过点A作x轴的垂线交x轴于点C.

在Rt△AOC中,OC=
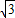 ,AC=1,
,AC=1,∴OA=
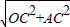 =2,∠AOC=30°,
=2,∠AOC=30°,∵将线段OA绕O点顺时针旋转30°得到线段OB,
∴∠AOB=30°,OB=OA=2,
∴∠BOC=60°.
过点B作x轴的垂线交x轴于点D.
在Rt△BOD中,BD=OB•sin∠BOD=
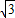 ,OD=
,OD= OB=1,
OB=1,∴B点坐标为(-1,
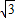 ),
),将x=-1代入y=-
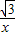 中,得y=
中,得y=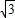 ,
,∴点B(-1,
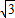 )在反比例函数y=-
)在反比例函数y=-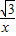 的图象上.
的图象上.(3)由y=-
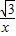 得xy=-
得xy=-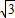 ,
,∵点P(m,
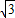 m+6)在反比例函数y=-
m+6)在反比例函数y=-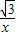 的图象上,其中m<0,
的图象上,其中m<0,∴m(
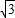 m+6)=-
m+6)=-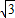 ,
,∴m2+2
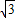 m+1=0,
m+1=0,∵PQ⊥x轴,∴Q点的坐标为(m,n).
∵△OQM的面积是
 ,
,∴
 OM•QM=
OM•QM= ,
,∵m<0,∴mn=-1,
∴m2n2+2
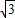 mn2+n2=0,
mn2+n2=0,∴n2-2
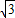 n=-1,
n=-1,∴n2-2
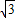 n+9=8.
n+9=8.点评:本题综合考查了运用待定系数法求反比例函数的解析式,旋转的性质,三角函数的定义,求代数式的值等知识,尤其是在最后一问中,没有必要求出n的具体值,而是将mn=-1作为一个整体代入,有一定的技巧性,使计算简便.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
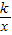 的图象经过点A(-
的图象经过点A(-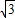 ,1).
,1).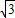 m+6)也在此反比例函数的图象上(其中m<0),过P点作x轴的垂线,交x轴于点M.若线段PM上存在一点Q,使得△OQM的面积是
m+6)也在此反比例函数的图象上(其中m<0),过P点作x轴的垂线,交x轴于点M.若线段PM上存在一点Q,使得△OQM的面积是 ,设Q点的纵坐标为n,求n2-2
,设Q点的纵坐标为n,求n2-2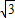 n+9的值.
n+9的值.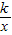 的图象经过点A(-
的图象经过点A(-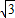 ,1).
,1).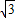 m+6)也在此反比例函数的图象上(其中m<0),过P点作x轴的垂线,交x轴于点M.若线段PM上存在一点Q,使得△OQM的面积是
m+6)也在此反比例函数的图象上(其中m<0),过P点作x轴的垂线,交x轴于点M.若线段PM上存在一点Q,使得△OQM的面积是 ,设Q点的纵坐标为n,求n2-2
,设Q点的纵坐标为n,求n2-2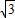 n+9的值.
n+9的值.