题目内容
如图①所示,在直角梯形ABCD中,∠BAD=90°,E是直线AB上一点,过E作直线//BC,交直线CD于点F.将直线向右平移,设平移距离BE为 (t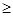 0),直角梯形ABCD被直线扫过的面积(图中阴影部份)为S,S关于的函数图象如图②所示,OM为线段,MN为抛物线的一部分,NQ为射线,N点横坐标为4.
0),直角梯形ABCD被直线扫过的面积(图中阴影部份)为S,S关于的函数图象如图②所示,OM为线段,MN为抛物线的一部分,NQ为射线,N点横坐标为4.

信息读取
(1)梯形上底的长AB= ;
(2) 直角梯形ABCD的面积= ;
图象理解
(3)写出图②中射线NQ表示的实际意义;
(4) 当 时,求S关于的函数关系式;
时,求S关于的函数关系式;
问题解决
(5)当t为何值时,直线l将直角梯形ABCD分成的两部分面积之比为1: 3.
(1) (2)S梯形ABCD=12(3)当平移距离BE大于等于4时,直角梯形ABCD被直线扫过的面积恒为12(4)S=-t2+8t-4(5)
(2)S梯形ABCD=12(3)当平移距离BE大于等于4时,直角梯形ABCD被直线扫过的面积恒为12(4)S=-t2+8t-4(5) 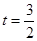 或
或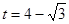
【解析】(1) .……1分
.……1分
(2)S梯形ABCD=12 .……1分
(3)射线NQ表示的实际意义:当平移距离BE大于等于4时,直角梯形ABCD被直线扫过的面积恒为12.……2分
(4)当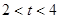 时,如下图所示,
时,如下图所示,

直角梯形ABCD被直线扫过的面积S=S直角梯形ABCD-SRt△DOF
 .……2分
.……2分
(5)①当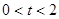 时,有
时,有
 ,解得
,解得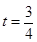 .……2分
.……2分
②当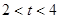 时,有
时,有
 ,
,
即 ,解得
,解得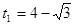 ,
,
 (舍去).……2分
(舍去).……2分
答:当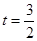 或
或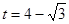 时,直线l将直角梯形ABCD分成的两部分面积之比为1: 3.
时,直线l将直角梯形ABCD分成的两部分面积之比为1: 3.
(1)根据图②可知,当0≤t≤2时,E在线段AB上运动(包括与A、B重合),在此期间E点运动了2秒,因此可求得AB的长为2.
(2)根据图形可知:当2<t<4时,E在AB的延长线上,且F在D点左侧,此期间E点运动了2秒,因此下底长为2+2=4,根据t=2时,重合部分的面积为8可求出梯形的高为4,因此梯形的面积为1/2 ×(2+4)×4=12.
(3)当t>4时,直线l与梯形没有交点,因此扫过的面积恒为梯形的面积12.
(4)当2<t<4时,直线扫过梯形的部分是个五边形,如果设直线l与AD的交点为0,那么重合部分的面积可用梯形的面积减去三角形OFD的面积来求得.梯形的面积在(2)中已经求得.三角形OFD中,底边DF=4-t,而DF上的高,可用DF的长和∠BCD的正切值求出,由此可得出S,t的函数关系式.
(5)本题要分情况讨论:
①当0<t<2时,重合部分的平行四边形的面积:直角梯形AEFD的面积=1:3,据此可求出t的值.
②当2<t<4时,重合部分的五边形的面积:三角形OFD的面积=3:1,由此可求出t的值.

 如图所示,在直角梯形ABCD中,AD∥BC,∠B=90°,EF是中位线,ED平分∠ADC,下面的结论:①CE平分∠BCD;②CD=AD+BC;③点E到CD的距离为
如图所示,在直角梯形ABCD中,AD∥BC,∠B=90°,EF是中位线,ED平分∠ADC,下面的结论:①CE平分∠BCD;②CD=AD+BC;③点E到CD的距离为| 1 |
| 2 |
| A、0个 | B、1个 | C、2个 | D、3个 |
 如图所示,在直角梯形ABCD中,∠ABC=90°,DC∥AB,BC=3,DC=4,AD=5,动点P从点B出发,由B→C→D→A沿边运动时,则△ABP的最大面积为
如图所示,在直角梯形ABCD中,∠ABC=90°,DC∥AB,BC=3,DC=4,AD=5,动点P从点B出发,由B→C→D→A沿边运动时,则△ABP的最大面积为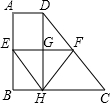 如图所示,在直角梯形ABCD中,AB⊥BC,AD=1,BC=3,CD=4,EF为梯形的中位线,DH为梯形的高且交EF于点G,下列结论:①G为EF的中点;②△EHF为等边三角形;③四边形EHCF为菱形;④S△BEH=S△CFH,其中正确的结论有( )
如图所示,在直角梯形ABCD中,AB⊥BC,AD=1,BC=3,CD=4,EF为梯形的中位线,DH为梯形的高且交EF于点G,下列结论:①G为EF的中点;②△EHF为等边三角形;③四边形EHCF为菱形;④S△BEH=S△CFH,其中正确的结论有( ) 如图所示,在直角梯形ABCD中,AD∥BC,∠A=90°,AB=12,BC=21,AD=16.动点P从点B出发,沿射线BC的方向以每秒2个单位长的速度运动,动点Q同时从点A出发,在线段AD上以每秒1个单位长的速度向点D运动,当其中一个动点到达端点时另一个动点也随之停止运动.设运动的时间为t(秒).
如图所示,在直角梯形ABCD中,AD∥BC,∠A=90°,AB=12,BC=21,AD=16.动点P从点B出发,沿射线BC的方向以每秒2个单位长的速度运动,动点Q同时从点A出发,在线段AD上以每秒1个单位长的速度向点D运动,当其中一个动点到达端点时另一个动点也随之停止运动.设运动的时间为t(秒).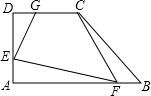 如图所示,在直角梯形ABCD中,∠A=∠D=90°,截取AE=BF=DG=x.已知AB=6,CD=3,AD=4.求四边形CGEF的面积S关于x的函数表达式和x的取值范围.
如图所示,在直角梯形ABCD中,∠A=∠D=90°,截取AE=BF=DG=x.已知AB=6,CD=3,AD=4.求四边形CGEF的面积S关于x的函数表达式和x的取值范围.