题目内容
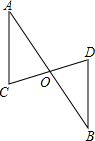如图，AB交CD于点O，点O分别是AB与CD的中点，则下列结论中错误的是（ ）分析：根据全等三角形的判定定理SAS证得△ACO≌△BDO，则由“全等三角形的对应边、对应角相等”得到∠A=∠B，AC=BD．再根据“内错角相等，两直线平行”推知AC∥BD．
解答：解：如图，∵AB交CD于点O，点O分别是AB与CD的中点，
∴AO=BO，CO=DO，
∴在△ACO与△BDO中，
，
∴△ACO≌△BDO（SAS），
∴∠A=∠B，AC=BD（故A、B选项正确），但是（∠A+∠B）不一定等于90°，所以C选项错误；
∴AC∥BD（故D选项正确）．
故选C．
∴AO=BO，CO=DO，
∴在△ACO与△BDO中，
|
∴△ACO≌△BDO（SAS），
∴∠A=∠B，AC=BD（故A、B选项正确），但是（∠A+∠B）不一定等于90°，所以C选项错误；
∴AC∥BD（故D选项正确）．
故选C．
点评：本题考查了全等三角形的判定与性质．在应用全等三角形的判定时，要注意三角形间的公共边、公共角以及对顶角．
练习册系列答案
名校课堂系列答案
相关题目
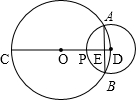如图，CD是⊙O的直径，以D为圆心的圆与⊙O交于A、B两点，AB交CD于点E，CD交⊙D于P，已知PC=6，PE：ED=2：1，则AB的长为（ ）
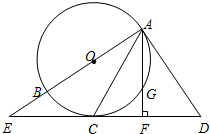如图，AB是⊙O的直径，CD是⊙O的切线，切点为C．延长AB交CD于点E．连接AC，作∠DAC=∠ACD，作AF⊥ED于点F，交⊙O于点G．
