题目内容
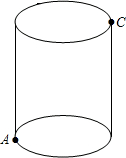 如图所示的圆柱体中底面圆的半径是
如图所示的圆柱体中底面圆的半径是| 2 | π |
分析:先将图形展开,再根据两点之间线段最短,由勾股定理可得出.
解答: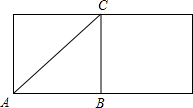 解:圆柱的侧面展开图是一个矩形,此矩形的长等于圆柱底面周长,C是边的中点,矩形的宽即高等于圆柱的母线长.
解:圆柱的侧面展开图是一个矩形,此矩形的长等于圆柱底面周长,C是边的中点,矩形的宽即高等于圆柱的母线长.
∵AB=π•
=2,CB=2.
∴AC=
=
=2
,
答:小虫爬行的最短路程是2
.
 解:圆柱的侧面展开图是一个矩形,此矩形的长等于圆柱底面周长,C是边的中点,矩形的宽即高等于圆柱的母线长.
解:圆柱的侧面展开图是一个矩形,此矩形的长等于圆柱底面周长,C是边的中点,矩形的宽即高等于圆柱的母线长.∵AB=π•
| 2 |
| π |
∴AC=
| AB2+BC2 |
| 8 |
| 2 |
答:小虫爬行的最短路程是2
| 2 |
点评:此题主要考查了平面展开图最短路径问题,此矩形的长等于圆柱底面周长,矩形的宽即高等于圆柱的母线长.本题就是把圆柱的侧面展开成矩形,“化曲面为平面”,用勾股定理解决.

练习册系列答案
相关题目
 如图所示的圆柱体中底面圆的半径是
如图所示的圆柱体中底面圆的半径是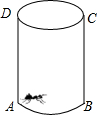 如图所示的圆柱体中底面圆的半径是
如图所示的圆柱体中底面圆的半径是
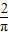 ,高为2,若一只小虫从A点出发沿着圆柱体的侧面爬行到C点,则小虫爬行的最短路程是 .(结果保留根号)
,高为2,若一只小虫从A点出发沿着圆柱体的侧面爬行到C点,则小虫爬行的最短路程是 .(结果保留根号)