题目内容
【题目】四边形ABCD的对角线交于点E,有AE=EC,BE=ED,以AB为直径的半圆过点E,圆心为O.
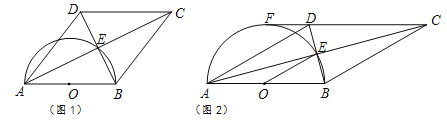
(1)利用图1,求证:四边形ABCD是菱形.
(2)如图2,若CD的延长线与半圆相切于点F,已知直径AB=8.
①连结OE,求△OBE的面积.
②求弧AE的长.
【答案】(1)证明见解析;(2)①4,②p.
【解析】试题分析: (1)利用对角线互相平分可先判断四边形ABCD为平行四边形,再利用直径对的圆周角是90°可得到AC⊥BD,就可判断是菱形.(2)①连接OF,可得OF为△ABD边AB上的高,可求得△ABD的面积为16,△AEB面积为△ABD的面积的一半,即等于8,△OEB的面积为△AEB面积的一半,即等于4;④过点D作DH⊥AB于点H.可得四边形OFDH为矩形,在Rt△ADH中利用三角函数可求得∠DAH=30°,进而可求得∠AOE的度数,弧AE的长度可求.
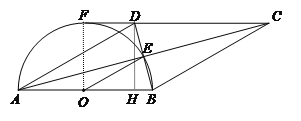
试题解析:(1)∵AE="EC,BE=ED," ∴四边形ABCD是平行四边形.∵AB为直径,且过点E,∴∠AEB=90°,即AC⊥BD.而四边形ABCD是平行四边形,∴四边形ABCD是菱形.(2)①连结OF.∵CD的延长线与半圆相切于点F,∴OF⊥CF.∵FC∥AB,∴OF即为△ABD的AB边上的高.S△ABD=AB×OF=×8×4=16.∵点O,E分别是AB,BD的中点,∴S△ABE=S△ABD=8,所以,S△OBE=S△ABE=4.②过点D作DH⊥AB于点H.∵AB∥CD,OF⊥CF,
∴FO⊥AB,∴∠F=∠FOB=∠DHO=90°.∴四边形OHDF为矩形,即DH=OF=4.在Rt△DAH中,sin∠DAB=![]() =,∴∠DAH=30°.∵点O,E分别为AB,BD中点,∴OE∥AD,∴∠EOB=∠DAH=30°.∴∠AOE=180°-∠EOB=150°.∴弧AE的长=
=,∴∠DAH=30°.∵点O,E分别为AB,BD中点,∴OE∥AD,∴∠EOB=∠DAH=30°.∴∠AOE=180°-∠EOB=150°.∴弧AE的长=![]() .
.

 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案【题目】二次函数y=ax2+bx+c的部分对应值如下表.利用二次函数的图象可知,当函数值y<0时,x的取值范围是
( )
x | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | 4 | 5 |
y | 12 | 5 | 0 | ﹣3 | ﹣4 | ﹣3 | 0 | 5 | 12 |
A. x<0或x>2 B. 0<x<2 C. x<﹣1或x>3 D. ﹣1<x<3