题目内容
（2012•思明区质检）如图，平行四边形ABCD中，AB=8，BC=10，∠B为锐角，tan∠B=| 4 | 3 |
（1）若点G在线段BC上，求△BEG与△CFG的周长之和；
（2）判断在点E的运动过程中，△AED与△CGD是否会相似？如果相似，请求出BE的长；如果不相似，请说明理由．
分析：（1）方法一：由三角形的周长公式知C△BEG+C△CFG=BE+CF+EF+BC，所以下一步求得线段BE、CF、EF和BC的长度即可；通过作辅助线CH构建矩形EFCH，利用矩形的对边相等的性质推知CF=EH，EF=CH；然后在Rt△BHC中，利用正切三角函数定义、勾股定理求得BH=6，CH=8，则EF=CH=8，BE+CF=BH=6；
方法二：设BE=3k．在Rt△BEG中，利用勾股定理，锐角三角函数的定义求得EG=4k，BG=5k；然后利用平行四边形ABCD的性质推知CG=BC-BG=10-5k，在Rt△CFG中，GF=8-4k，CF=6-3k；最后由三角形的周长公式求得C△BEG+C△CFG=24；
（2）需要分类讨论：①当0＜BE＜6时，△AED与△CGD相似；②当BE=6时，点G与点C重合，不存在△CGD与△AED相似；③当6＜BE＜8时，不存在△CGD与△AED相似．
方法二：设BE=3k．在Rt△BEG中，利用勾股定理，锐角三角函数的定义求得EG=4k，BG=5k；然后利用平行四边形ABCD的性质推知CG=BC-BG=10-5k，在Rt△CFG中，GF=8-4k，CF=6-3k；最后由三角形的周长公式求得C△BEG+C△CFG=24；
（2）需要分类讨论：①当0＜BE＜6时，△AED与△CGD相似；②当BE=6时，点G与点C重合，不存在△CGD与△AED相似；③当6＜BE＜8时，不存在△CGD与△AED相似．
解答：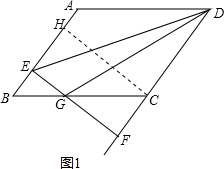
解：（1）方法一：如图1，过点C作CH⊥AB于H，
∵C△BEG=BE+EG+BG，C△CFG=CF+FG+CG，
∴C△BEG+C△CFG=BE+CF+EF+BC；
在平行四边形ABCD中，AB∥CD，EF⊥AB，
∴∠EFC=∠BEF=90°，又CH⊥AB，
∴四边形EFCH为矩形．
∴CF=EH，EF=CH；
在Rt△BHC中，BC=10，tan∠B=
，
可求得BH=6，CH=8，
∴EF=CH=8，BE+CF=BH=6．
∴C△BEG+C△CFG=6+8+10=24；
方法二：设BE=3k．
∵tan∠B=
，
∴
=
，
∴EG=4k，BG=5k；
在平行四边形ABCD中，∵AB∥CD，EF⊥AB，
∴∠BCF=∠B，CG=BC-BG=10-5k，∠EFC=∠BEF=90°．
∴在Rt△CFG中，GF=8-4k，CF=6-3k，
∴C△BEG+C△CFG=（BE+EG+BG）+（CF+FG+CG）=（3k+4k+5k）+（6-3k+8-4k+10-5k）
=24；
（2）①当0＜BE＜6，即点G在线段BC上时，设BE=3k，
∵tan∠B=
，
∴EG=4k，BG=5k，CG=10-5k，CD=AB=8．
∵∠A=∠DCG，
∴要使△AED与△CGD相似，需满足
=
或
=
．
当
=
时，
=
，
解得k=
，
此时，BE=
，满足0＜BE＜6．
当
=
时，
=
，
解得k1=0或 k2=
…（8分）
此时，BE=0或14，不满足0＜BE＜6；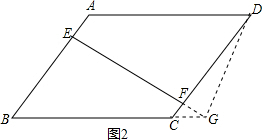
∴当 BE=
时，△AED与△CGD相似．
②当BE=6，即点G与点C重合时，不存在△CGD与△AED相似．
③当6＜BE＜8，即点G在射线BC上时，如图2，
∵AB∥CD，AD∥BC，∠B是锐角
∴∠A是钝角，
又∵∠DCG=∠B，
∴∠DCG也是锐角，
∴∠A≠∠DCG．
∵∠DCB＞∠CDG，∠DCB＞∠DGC，
又∵∠A=∠DCB
∴∠A≠∠CDG，且∠A≠∠DGC，
∴当6＜BE＜8时，不存在△CGD与△AED相似．
综上所述，当BE=
时，△AED与△CGD相似．
解：（1）方法一：如图1，过点C作CH⊥AB于H，∵C△BEG=BE+EG+BG，C△CFG=CF+FG+CG，
∴C△BEG+C△CFG=BE+CF+EF+BC；
在平行四边形ABCD中，AB∥CD，EF⊥AB，
∴∠EFC=∠BEF=90°，又CH⊥AB，
∴四边形EFCH为矩形．
∴CF=EH，EF=CH；
在Rt△BHC中，BC=10，tan∠B=
| 4 |
| 3 |
可求得BH=6，CH=8，
∴EF=CH=8，BE+CF=BH=6．
∴C△BEG+C△CFG=6+8+10=24；
方法二：设BE=3k．
∵tan∠B=
| 4 |
| 3 |
∴
| EG |
| BE |
| 4 |
| 3 |
∴EG=4k，BG=5k；
在平行四边形ABCD中，∵AB∥CD，EF⊥AB，
∴∠BCF=∠B，CG=BC-BG=10-5k，∠EFC=∠BEF=90°．
∴在Rt△CFG中，GF=8-4k，CF=6-3k，
∴C△BEG+C△CFG=（BE+EG+BG）+（CF+FG+CG）=（3k+4k+5k）+（6-3k+8-4k+10-5k）
=24；
（2）①当0＜BE＜6，即点G在线段BC上时，设BE=3k，
∵tan∠B=
| 4 |
| 3 |
∴EG=4k，BG=5k，CG=10-5k，CD=AB=8．
∵∠A=∠DCG，
∴要使△AED与△CGD相似，需满足
| AE |
| CG |
| AD |
| CD |
| AE |
| CD |
| AD |
| CG |
当
| AE |
| CG |
| AD |
| CD |
| 8-3k |
| 10-5k |
| 10 |
| 8 |
解得k=
| 18 |
| 13 |
此时，BE=
| 54 |
| 13 |
当
| AE |
| CD |
| AD |
| CG |
| 8-3k |
| 8 |
| 10 |
| 10-5k |
解得k1=0或 k2=
| 14 |
| 3 |
此时，BE=0或14，不满足0＜BE＜6；
∴当 BE=
| 54 |
| 13 |
②当BE=6，即点G与点C重合时，不存在△CGD与△AED相似．
③当6＜BE＜8，即点G在射线BC上时，如图2，
∵AB∥CD，AD∥BC，∠B是锐角
∴∠A是钝角，
又∵∠DCG=∠B，
∴∠DCG也是锐角，
∴∠A≠∠DCG．
∵∠DCB＞∠CDG，∠DCB＞∠DGC，
又∵∠A=∠DCB
∴∠A≠∠CDG，且∠A≠∠DGC，
∴当6＜BE＜8时，不存在△CGD与△AED相似．
综上所述，当BE=
| 54 |
| 13 |
点评：本题考查了相似综合题．此题涉及到的知识点有平行四边形的性质、矩形的判定与性质、勾股定理以及锐角三角函数的定义．解答（2）时，要分类讨论，以防漏解．
练习册系列答案
相关题目