题目内容
已知直角坐标系中有A(1,4),B(2,3),C(2,-1),D(-1,1)四点,则经过A,C两点的直线L1与经过B,D两点的直线L2的交点可以看做是方程组________的解.
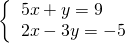
分析:可用待定系数法求出直线L1与直线L2的解析式,由于函数图象交点坐标为两函数解析式组成的方程组的解,因此所求的方程组即为联立直线L1与L2的解析式所得的方程组.
解答:设直线L1的解析式为y=kx+b,根据题意,得:
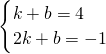 解得:
解得: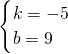 ;
;则L1的函数解析式是y=-5x+9;同理可以求出直线L2的解析式是y=
 x+
x+ ;
;则直线L1与直线L2的交点可以看做是方程组
 的解.
的解.点评:在同一平面直角坐标系中,两个一次函数图象的交点坐标就是相应的二元一次方程组的解.反过来,以二元一次方程组的解为坐标的点,一定是相应的两个一次函数的图象的交点.

练习册系列答案
相关题目