题目内容
同一个圆的内接正方形和外切正六边形的边长之比为 .
【答案】分析:圆的半径是内接圆正方形半径,是外切正六边形的边心距;设圆的半径是R,则可表示出两个多边形的边长,进而求解.
解答:解:设此圆的半径为R,
则它的内接正方形的边长为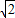 R,
R,
它的外切正六边形的边长为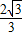 R,
R,
内接正方形和外切正六边形的边长比为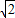 R:
R: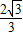 R=
R=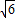 :2.
:2.
故答案为: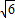 :2.
:2.
点评:解决圆的相关问题一定要结合图形,掌握基本的图形变换.找出内接正方形与外切正六边形的边长关系,是解决问题的关键.
解答:解:设此圆的半径为R,
则它的内接正方形的边长为
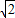 R,
R,它的外切正六边形的边长为
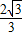 R,
R,内接正方形和外切正六边形的边长比为
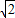 R:
R: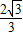 R=
R=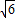 :2.
:2.故答案为:
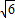 :2.
:2.点评:解决圆的相关问题一定要结合图形,掌握基本的图形变换.找出内接正方形与外切正六边形的边长关系,是解决问题的关键.

练习册系列答案
相关题目