题目内容
如图,直线 ,点A1坐标为(1,0),过点A1作x轴的垂线交直线于点B1,以原点O为圆心,OB1长为半径画弧交x轴于点A2;再过点A2作x轴的垂线交直线于点B2,以原点O为圆心,OB2长为半径画弧交x轴于点A3,…,按此做法进行下去,点A4的坐标为 ,点An .
,点A1坐标为(1,0),过点A1作x轴的垂线交直线于点B1,以原点O为圆心,OB1长为半径画弧交x轴于点A2;再过点A2作x轴的垂线交直线于点B2,以原点O为圆心,OB2长为半径画弧交x轴于点A3,…,按此做法进行下去,点A4的坐标为 ,点An .
【答案】分析:由直线解析式求出B1点的坐标,解直角三角形得出∠B1OA1=30°,由此可发现,OA2=OB1=OA1÷cos30°= OA1,同理OA3=
OA1,同理OA3=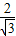 OA2=(
OA2=( )2OA1,OA4=
)2OA1,OA4=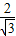 OA3=(
OA3=(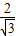 )3OA1,…,由此得出一般规律.
)3OA1,…,由此得出一般规律.
解答:解:由A1坐标为(1,0),可知OA1=1,
把x=1代入直线y=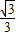 x中,得y=
x中,得y= ,即A1B1=
,即A1B1=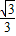 ,
,
tan∠B1OA1=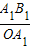 =
=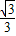 ,所以,∠B1OA1=30°,
,所以,∠B1OA1=30°,
则OA2=OB1=OA1÷cos30°= OA1=
OA1= ,
,
OA3=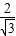 OA2=(
OA2=(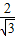 )2,OA4=
)2,OA4=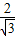 OA3=(
OA3=( )3,
)3,
故点A4的坐标为( ,0),点An((
,0),点An(( )n-1,0).
)n-1,0).
故答案为:(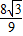 ,0),((
,0),((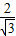 )n-1,0).
)n-1,0).
点评:本题考查了一次函数的综合运用.关键是由直线解析式求出直线与x轴正方向的夹角为30°,再依次求OA2,OA3,OA4,…的长,得出一般规律.
 OA1,同理OA3=
OA1,同理OA3=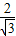 OA2=(
OA2=( )2OA1,OA4=
)2OA1,OA4=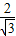 OA3=(
OA3=(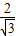 )3OA1,…,由此得出一般规律.
)3OA1,…,由此得出一般规律.解答:解:由A1坐标为(1,0),可知OA1=1,
把x=1代入直线y=
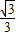 x中,得y=
x中,得y= ,即A1B1=
,即A1B1=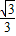 ,
,tan∠B1OA1=
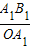 =
=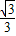 ,所以,∠B1OA1=30°,
,所以,∠B1OA1=30°,则OA2=OB1=OA1÷cos30°=
 OA1=
OA1= ,
,OA3=
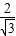 OA2=(
OA2=(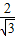 )2,OA4=
)2,OA4=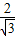 OA3=(
OA3=( )3,
)3,故点A4的坐标为(
 ,0),点An((
,0),点An(( )n-1,0).
)n-1,0).故答案为:(
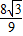 ,0),((
,0),((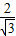 )n-1,0).
)n-1,0).点评:本题考查了一次函数的综合运用.关键是由直线解析式求出直线与x轴正方向的夹角为30°,再依次求OA2,OA3,OA4,…的长,得出一般规律.

练习册系列答案
相关题目
 ,点A1坐标为(1,0),过点A1作x的垂线交直线于点B1,以原点O为圆心,OB1长为半径画弧交x轴于点A2;再过点A2x的垂线交直线于点B2,以原点O为圆心,OB2长为半径画弧交x轴于点A3,…,按此做法进行下去,点A5的坐标为( , ).
,点A1坐标为(1,0),过点A1作x的垂线交直线于点B1,以原点O为圆心,OB1长为半径画弧交x轴于点A2;再过点A2x的垂线交直线于点B2,以原点O为圆心,OB2长为半径画弧交x轴于点A3,…,按此做法进行下去,点A5的坐标为( , ).
 ,点A1坐标为(1,0),过点A1作x的垂线交直线于点B1,以原点O为圆心,OB1长为半径画弧交x轴于点A2;再过点A2x的垂线交直线于点B2,以原点O为圆心,OB2长为半径画弧交x轴于点A3,…,按此做法进行下去,点A5的坐标为( , ).
,点A1坐标为(1,0),过点A1作x的垂线交直线于点B1,以原点O为圆心,OB1长为半径画弧交x轴于点A2;再过点A2x的垂线交直线于点B2,以原点O为圆心,OB2长为半径画弧交x轴于点A3,…,按此做法进行下去,点A5的坐标为( , ).
 ,点A1坐标为(1,0),过点A1作x轴的垂线交直线于点B1,以原点O为圆心,OB1长为半径画弧交x轴于点A2;再过点A2作x轴的垂线交直线于点B2,以原点O为圆心,OB2长为半径画弧交x轴于点A3,…,按此做法进行下去,点A4的坐标为 ,点An .
,点A1坐标为(1,0),过点A1作x轴的垂线交直线于点B1,以原点O为圆心,OB1长为半径画弧交x轴于点A2;再过点A2作x轴的垂线交直线于点B2,以原点O为圆心,OB2长为半径画弧交x轴于点A3,…,按此做法进行下去,点A4的坐标为 ,点An .
 ,点A1坐标为(1,0),过点A1作x的垂线交直线于点B1,以原点O为圆心,OB1长为半径画弧交x轴于点A2;再过点A2x的垂线交直线于点B2,以原点O为圆心,OB2长为半径画弧交x轴于点A3,…,按此做法进行下去,点A5的坐标为( , ).
,点A1坐标为(1,0),过点A1作x的垂线交直线于点B1,以原点O为圆心,OB1长为半径画弧交x轴于点A2;再过点A2x的垂线交直线于点B2,以原点O为圆心,OB2长为半径画弧交x轴于点A3,…,按此做法进行下去,点A5的坐标为( , ).