题目内容
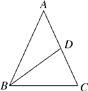
【题目】如图①,AB=AC,BD、CD分别平分∠ABC和∠ACB.问:(答题时,注意书写整洁)
(1)图①中有几个等腰三角形?(写出来,不需要证明)
(2)过D点作EF∥BC,交AB于E,交AC于F,如图②,图中增加了几个等腰三角形,选一个进行证明.
(3)如图③,若将题中的△ABC改为不等边三角形,其他条件不变,图中有几个等腰三角形?线段EF与BE、CF有什么关系?(写出来,不需要证明)

【答案】(1)有两个等腰三角形:△ABC,△BDC.(2)增加了三个等腰三角形:△EBD,△FDC,△AEF,证明见解析;(3)有两个等腰三角形:△EBD,△FDC.EF=BE+CF,理由见解析
【解析】
(1)由条件可证得∠DBC=∠DCB,所以共有两个等腰三角形;
(2)由平行和角平分线的性质可得∠EDB=∠EBD,∠FDC=∠FCD,且AE=AF,所以增加了三个等腰三角形;
(3)此时同②只能得出∠EDB=∠EBD,∠FDC=∠FCD,即只有两个等腰三角形,且EF=BE+FC.
(1)∵AB=AC,
∴∠ABC=∠ACB,
∵BD、CD分别是角平分线,
∴∠DBC=12∠ABC=12∠ACB=∠DCB,
∴DB=DC,
∴△BDC是等腰三角形,
即在图1中共有两个等腰三角形;
(2)∵EF∥BC,
∴∠EDB=∠DBC,
∵BD平分∠ABC,
∴∠DBE=∠DBC,
∴∠DBE=∠EDB,
∴EB=ED,
∴△EBD为等腰三角形,同理△FDC为等腰三角形,
∵EF∥BC,
∴∠AEF=∠AFE,
∵AB=AC,
∴△AEF为等腰三角形,
即在图2中增加了三个等腰三角形;
(3)同(2)可证明得△EBD为等腰三角形,△FDC为等腰三角形,
所以EF=BE+CF,
即只有两个等腰三角形.

练习册系列答案
相关题目