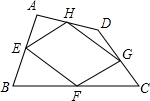
题目内容
(1)顺次连接任意四边形各边中点构成的四边形是(2)顺次连接对角线相等的四边形的各边中点,构成的四边形是
(3)顺次连接对角线互相垂直的四边形的各边中点构成的四边形是
分析:(1)连接任意四边形的中点,如图,连接AC,根据三角形的中位线定理,可以证得HG=FE=
AC,并且HG∥EF,所以利用平行四边形的判定定理可知,该中点四边形是平行四边形.
(2)在(1)的基础上,易证平行四边形GHBF的一组邻边相等,所以根据菱形的定义可知该中点四边形是菱形.
(3)在(1)的基础上,易证平行四边形GHBF中有一个角是直角,所以根据矩形的定义可知该中点四边形是矩形.
| 1 |
| 2 |
(2)在(1)的基础上,易证平行四边形GHBF的一组邻边相等,所以根据菱形的定义可知该中点四边形是菱形.
(3)在(1)的基础上,易证平行四边形GHBF中有一个角是直角,所以根据矩形的定义可知该中点四边形是矩形.
解答:解:(1)如图所示,任意四边形ABCD中,E、F、G、H分别为各边的中点,求四边形EFGH的形状.
连接AC,
∵E、F、G、H分别为各边的中点,
∴HG、EF分别为△ACD与△ABC的中位线,
∴HG∥AC∥EF,HG=EF=
AC,
∴四边形EFGH是平行四边形;
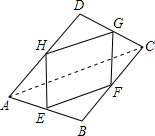
(2)如图所示,四边形ABCD的对角线AC=BD,E、F、G、H分别为各边的中点,求四边形EFGH的形状.
连接AC、BD,
∵E、F、G、H分别为各边的中点,
∴EH、GF分别为△ABD与△BCD的中位线,
∴EH∥BD∥GF,EH=GF=
BD,
∴四边形EFGH是平行四边形,
同理可得,HG=EF=
AC,
∵AC=BD,
∴EH=GF,
∴四边形EFGH是菱形;
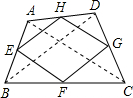
(3)如图所示,四边形ABCD的对角线AC⊥BD,E、F、G、H分别为各边的中点,求四边形EFGH的形状.
解:连接AC、BD,
∵E、F、G、H分别为各边的中点,
∴EH、GF分别为△ABD与△BCD的中位线,
∴EH∥BD∥GF,EH=GF=
BD,
∴四边形EFGH是平行四边形,
同理可得,HG∥AC∥EF,
∵AC⊥BD,
∴HG⊥BD⊥EH,
∴四边形EFGH是矩形.
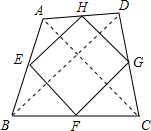
故答案分别为平行四边形、菱形、矩形.
连接AC,
∵E、F、G、H分别为各边的中点,
∴HG、EF分别为△ACD与△ABC的中位线,
∴HG∥AC∥EF,HG=EF=
| 1 |
| 2 |
∴四边形EFGH是平行四边形;

(2)如图所示,四边形ABCD的对角线AC=BD,E、F、G、H分别为各边的中点,求四边形EFGH的形状.
连接AC、BD,
∵E、F、G、H分别为各边的中点,
∴EH、GF分别为△ABD与△BCD的中位线,
∴EH∥BD∥GF,EH=GF=
| 1 |
| 2 |
∴四边形EFGH是平行四边形,
同理可得,HG=EF=
| 1 |
| 2 |
∵AC=BD,
∴EH=GF,
∴四边形EFGH是菱形;

(3)如图所示,四边形ABCD的对角线AC⊥BD,E、F、G、H分别为各边的中点,求四边形EFGH的形状.
解:连接AC、BD,
∵E、F、G、H分别为各边的中点,
∴EH、GF分别为△ABD与△BCD的中位线,
∴EH∥BD∥GF,EH=GF=
| 1 |
| 2 |
∴四边形EFGH是平行四边形,
同理可得,HG∥AC∥EF,
∵AC⊥BD,
∴HG⊥BD⊥EH,
∴四边形EFGH是矩形.

故答案分别为平行四边形、菱形、矩形.
点评:本题考查的是三角形中位线定理,即三角形的中位线平行于底边且等于底边的一半.解答此题的关键是根据题意画出图形,利用数形结合解答.

练习册系列答案
相关题目
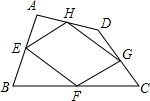 顺次连接任意四边形ABCD各边中点,所得的四边形EFGH是中点四边形.下列四个叙述:①中点四边形EFGH一定是平行四边形;②当四边形ABCD是矩形时,中点四边形EFGH也是矩形;③当中点四边形EFGH是菱形时,四边形ABCD是矩形;④当四边形ABCD是正方形时,中点四边形EFGH也是正方形.其中正确的是
顺次连接任意四边形ABCD各边中点,所得的四边形EFGH是中点四边形.下列四个叙述:①中点四边形EFGH一定是平行四边形;②当四边形ABCD是矩形时,中点四边形EFGH也是矩形;③当中点四边形EFGH是菱形时,四边形ABCD是矩形;④当四边形ABCD是正方形时,中点四边形EFGH也是正方形.其中正确的是 顺次连接任意四边形ABCD各边中点,所得的四边形EFGH是中点四边形.下列四个叙述:①中点四边形EFGH一定是平行四边形;②当四边形ABCD是矩形时,中点四边形EFGH也是矩形;③当中点四边形EFGH是菱形时,四边形ABCD是矩形;④当四边形ABCD是正方形时,中点四边形EFGH也是正方形.其中正确的是________(只填代号).
顺次连接任意四边形ABCD各边中点,所得的四边形EFGH是中点四边形.下列四个叙述:①中点四边形EFGH一定是平行四边形;②当四边形ABCD是矩形时,中点四边形EFGH也是矩形;③当中点四边形EFGH是菱形时,四边形ABCD是矩形;④当四边形ABCD是正方形时,中点四边形EFGH也是正方形.其中正确的是________(只填代号).