题目内容
如图，△AOB中，OA=OB=10，∠AOB=120°，以O为圆心，5为半径的⊙O与OA、OB相交．求证：AB是⊙O的切线．
分析：如图，过点O作OD⊥AB于点D．根据等腰三角形AOB的性质知OD是∠AOB的角平分线，然后利用勾股定理求得OD等于该圆的半径，则AB是圆O的切线．
解答：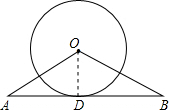
证明：如图，过点O作OD⊥AB于点D．
∵在△AOB中，OA=OB=10，
∴OD是∠AOB的角平分线，
∴∠AOD=
∠AOB=60°，则∠OAD=30°，
∴OD=
OA=5．
∵⊙O的半径是5，
∴点OD是⊙O的半径，
∴AB是⊙O的切线．
证明：如图，过点O作OD⊥AB于点D．∵在△AOB中，OA=OB=10，
∴OD是∠AOB的角平分线，
∴∠AOD=
| 1 |
| 2 |
∴OD=
| 1 |
| 2 |
∵⊙O的半径是5，
∴点OD是⊙O的半径，
∴AB是⊙O的切线．
点评：本题考查了切线的判定．解答此题时，充分利用了等腰三角形“三合一”的性质．
练习册系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
E、F
2、如图，△AOB中，∠B=30度．将△AOB绕点O顺时针旋转52°得到△A′OB′，边A′B′与边OB交于点C（A′不在OB上），则∠A′CO的度数为（ ）
如图，△AOB中，OA=3cm，OB=1cm，将△AOB绕点O逆时针旋转90°到△A′OB′，那么AB扫过的区域（图中阴影部分）的面积是
如图，△AOB中，OA=OB，∠AOB=90゜，BD平分∠ABO交OA于D，AE⊥BD于E．