题目内容
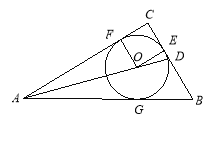
【题目】如图,![]() ,⊙
,⊙![]() 是Rt△
是Rt△![]() 的内切圆,分别切
的内切圆,分别切![]() 于点
于点![]() ,连接
,连接![]() .
.![]() 的延长线交
的延长线交![]() 于点
于点![]() ,
,![]() .
.
(1)求证:四边形![]() 为正方形;
为正方形;
(2)求⊙![]() 的半径;
的半径;
(3)求![]() 的长.
的长.
【答案】(1)答案见解析;(2)r=1.5;(3)AB=7.5
【解析】
试题分析:(1)根据内接圆得出矩形,然后根据OE=OF得出正方形;(2)根据正方形得出△OED∽△ACD,从而得出半径;(3)根据内切圆得出DE=0.5,设BD=c,则DE=x+0.5,根据AG=AF=4.5则AB=5+x,根据勾股定理求出AB的长度.
试题解析:(1)因为⊙O是Rt△ABC的内接圆,分别切BC,AC,AB 于点E,F,G
∴∠CFO=∠OEC=90°
∵∠C=90°.∴则四边形OECF为 矩形,
又∵OE=OF=r ∴四边形OECF为 正方形
(2)由四边形OECF为 正方形
∴OE//AC ,CE=CF=r
∴△OED∽△ACD
∴![]()
∴![]()
解得:r=![]()
(3)⊙![]() 是Rt△
是Rt△![]() 的内切圆,由(2)得DE=
的内切圆,由(2)得DE=![]() ,设BD=x,则BE=BG=x+
,设BD=x,则BE=BG=x+![]()
∵AG=AF=![]() ,∴AB=5+x ,
,∴AB=5+x ,
由![]() 得
得![]()
解得:x=![]()
∴AB =![]()

练习册系列答案
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目