题目内容
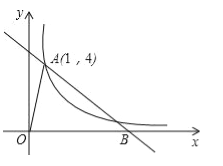
【题目】如图,直线y= ![]() x+6分别与x轴、y轴交于A、B两点:直线y=
x+6分别与x轴、y轴交于A、B两点:直线y= ![]() x与AB于点C,与过点A且平行于y轴的直线交于点D.点E从点A出发,以每秒1个单位的进度沿x轴向左运动.过点E作x轴的垂线,分別交直线AB、OD于P、Q两点,以PQ为边向右作正方形PQMN.设正方形PQMN与△ACD重叠的图形的周长为L个单位长度,点E的运动时间为t(秒).
x与AB于点C,与过点A且平行于y轴的直线交于点D.点E从点A出发,以每秒1个单位的进度沿x轴向左运动.过点E作x轴的垂线,分別交直线AB、OD于P、Q两点,以PQ为边向右作正方形PQMN.设正方形PQMN与△ACD重叠的图形的周长为L个单位长度,点E的运动时间为t(秒).
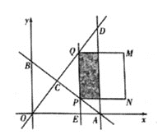
(1)直接写出点C和点A的坐标.
(2)若四边形OBQP为平行四边形,求t的值.
(3)0<t<5时,求L与t之间的函数解析式.
【答案】(1)![]() ,
,![]() ;(2)2;(3)
;(2)2;(3)![]() .
.
【解析】
(1)把y= ![]() x+6和 y=
x+6和 y= ![]() x联立组成方程组,解方程组求得方程组的解,即可得点C的坐标;在直线y=
x联立组成方程组,解方程组求得方程组的解,即可得点C的坐标;在直线y= ![]() x+6中,令y=0,求得x的值,即可得点A的坐标;(2)用t表示出点P、Q的坐标,求得PQ的长,由条件可知,BO∥QP,若使四边形OBQP为平行四边形,必须满足OB=QP,由此可得
x+6中,令y=0,求得x的值,即可得点A的坐标;(2)用t表示出点P、Q的坐标,求得PQ的长,由条件可知,BO∥QP,若使四边形OBQP为平行四边形,必须满足OB=QP,由此可得![]() ,即可求得t值;(3)由题意可知,正方形PQMN与△ACD重叠的图形是矩形,由此求得L与t之间的函数解析式即可.
,即可求得t值;(3)由题意可知,正方形PQMN与△ACD重叠的图形是矩形,由此求得L与t之间的函数解析式即可.
(1)C的坐标为( ![]() ),A的坐标为(8,0);
),A的坐标为(8,0);
(2)∵点B直线y= ![]() x+6与y轴的交点,
x+6与y轴的交点,
∴B(0,6),
∴OB=6,
∵A的坐标为(8,0),
∴OA=8,
由题意可得,OE=8-t,
∴P(8-t,![]() ),Q(8-t,
),Q(8-t,![]() )
)
∴![]() =10-2t,
=10-2t,
由条件可知,BO∥QP,若使四边形OBQP为平行四边形,必须满足OB=QP,
所以有 ![]() ,解得t=2;
,解得t=2;
(3)当0<t<5时, ![]() .
.

 快乐暑假暑假能力自测中西书局系列答案
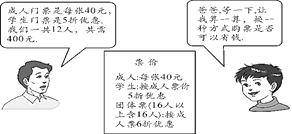
快乐暑假暑假能力自测中西书局系列答案【题目】某学校2019学年举行席地绘画大赛.共收到绘画作品480件,其中的优秀作品评出了一、二、三等奖.
占获奖总数的几分之几 | 获奖作品的件数 | |
一等奖 |
| b |
二等奖 |
| c |
三等奖 | a | 96 |
(1)则a= ;b= ;c= ;
(2)学校决定为获一等奖同学每人购买一个书包,获得二等奖同学每人购买一个文具盒,获得三等奖同学每人购买一支钢笔,并且每位获奖同学颁发一个证书,已知文具盒单价是书包单价的![]() ,证书的单价是文具盒单价的
,证书的单价是文具盒单价的![]() ,钢笔的单介是文具盒单价的
,钢笔的单介是文具盒单价的![]() ,学校购买书包、文具盒、钢笔共用4000元,那么学校购买证书共用了多少元?
,学校购买书包、文具盒、钢笔共用4000元,那么学校购买证书共用了多少元?
【题目】“元旦”期间,某文具店购进 ![]() 只两种型号的文具进行销售,其进价和售价如表:
只两种型号的文具进行销售,其进价和售价如表:
型号 | 进价(元/只) | 售价(元/只) |
A型 | 10 | 12 |
B型 | 15 | 23 |
(1)该店用 ![]() 元可以购进A,B两种型号的文具各多少只?
元可以购进A,B两种型号的文具各多少只?
(2)在(![]() )的条件下,若把所购进A,B两种型号的文具全部销售完,利润率有没有超过
)的条件下,若把所购进A,B两种型号的文具全部销售完,利润率有没有超过 ![]() ?请你说明理由.
?请你说明理由.