题目内容
【题目】如图,在△ABF中,以AB为直径的圆分别交边AF、BF于C、E两点,CD⊥AF.AC是∠DAB的平分线, 
(1)求证:直线CD是⊙O的切线.
(2)求证:△FEC是等腰三角形.
【答案】
(1)解:连接OC,则∠CAO=∠ACO,
又∠FAC=∠CAO
∴∠FAC=∠ACO,
∴AF∥CO,
而CD⊥AF,
∴CO⊥CD,
即直线CD是⊙O的切线
(2)解:∵AB是⊙O的直径,
∴∠ACB=90°
又∠FAC=∠CAO
∴AF=AB(三线合一),
∴∠F=∠B,
∵四边形EABC是⊙O的内接四边形,
∵∠FEC+∠AEC=180°,∠B+∠AEC=180°
∴∠FEC=∠B
∴∠F=∠FEC,
即EC=FC
所以△FEC是等腰三角形.
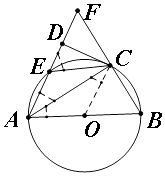
【解析】(1)先判断出∠FAC=∠ACO,进而得出AF∥CO,即可得出结论;(2)先用等腰三角形的三线合一得出AF=AB.再用同角的补角相等得出∠FEC=∠B 即可得出结论.
【考点精析】根据题目的已知条件,利用等腰三角形的判定和圆周角定理的相关知识可以得到问题的答案,需要掌握如果一个三角形有两个角相等,那么这两个角所对的边也相等(简称:等角对等边).这个判定定理常用于证明同一个三角形中的边相等;顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目