题目内容
（2010•静安区二模）解方程：
-
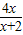=5．
【答案】分析：此题应先设
=y，将原分式方程化为y2-4y-5=0解得y1=-1，y2=5，再反代求出x的值．
解答：解：设
=y，（1分）
原方程可化为y2-4y-5=0，（3分）
（y+1）（y-5）=0，（4分）
y1=-1，y2=5．（5分）
当y=-1时，
=-1，x=-1（7分）
当y=5时，
=5，x=-
（9分）
经检验：x=-1，x=-
都是原方程的根．（10分）
所以原方程的根是x=-1，x=-
．
点评：本题主要考查用换元法解分式方程，求出结果一定要注意必须检验．
=y，将原分式方程化为y2-4y-5=0解得y1=-1，y2=5，再反代求出x的值．解答：解：设
=y，（1分）原方程可化为y2-4y-5=0，（3分）
（y+1）（y-5）=0，（4分）
y1=-1，y2=5．（5分）
当y=-1时，
=-1，x=-1（7分）当y=5时，
=5，x=-（9分）经检验：x=-1，x=-
都是原方程的根．（10分）所以原方程的根是x=-1，x=-
．点评：本题主要考查用换元法解分式方程，求出结果一定要注意必须检验．
练习册系列答案
小题狂做系列答案
相关题目
-
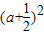+（a+1）-1+（a-1）-1，其中a=
．