题目内容
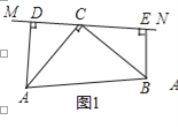
【题目】(10分)在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E,
证明:DE=AD+BE;
【答案】详见解析.
【解析】
试题分析:由∠ACB=90°,得∠ACD+∠BCE=90°,而AD⊥MN于D,BE⊥MN于点E,则∠ADC=∠CEB=90°,根据等角的余角相等得到∠ACD=∠CBE,易得△ADC≌△CEB,所以AD=CE,DC=BE,即可得到DE=DC+CE=BE+AD.
试题解析:证明:∵∠ACB=90°,
∴∠ACD+∠BCE=90°,
而AD⊥MN于D,BE⊥MN于点E,
∴∠ADC=∠CEB=90°,
∴∠ACD+∠BCE=90°∠BCE+∠CBE=90°,
∴∠ACD=∠CBE.
在△ADC和△CEB中,
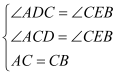
∴△ADC≌△CEB,
∴AD=CE,DC=BE,
∴DE=DC+CE=BE+AD;

练习册系列答案
相关题目

