题目内容
【题目】如图,菱形ABCD的边长为4,∠DAB=60°,E为BC的中点,在对角线AC上存在一点P,使△PBE的周长最小,则△PBE的周长的最小值为 ( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】C
【解析】
如下图,△BEP的周长=BE+BP+EP,其中BE是定值,只需要BP+PE为最小值即可,过点E作AC的对称点F,连接FB,则FB就是BP+PE的最小值.
如下图,过点E作AC的对称点F,连接FB,FE,过点B作FE的垂线,交FE的延长线于点G
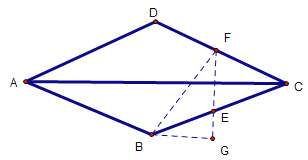
∵菱形ABCD的边长为4,点E是BC的中点
∴BE=2
∵∠DAB=60°,∴∠FCE=60°
∵点F是点E关于AC的对称点
∴根据菱形的对称性可知,点F在DC的中点上
则CF=CE=2
∴△CFE是等边三角形,∴∠FEC=60°,EF=2
∴∠BEG=60°
∴在Rt△BEG中,EG=1,BG=![]()
∴FG=1+2=3
∴在Rt△BFG中,BF=![]() =2
=2![]()
根据分析可知,BF=PB+PE
∴△PBE的周长=2![]()
故选:C

练习册系列答案
相关题目