题目内容
如图所示，为了测量一棵树AB的高度，测量者在D点立一高CD=2m的标杆，现测量者从E处可以看到杆顶C与树顶A在同一条直线上，如果测得BD=20m，FD=4m，EF=1.8m，则树AB的高度为 m．
【答案】分析：过E作AB的垂线，然后在构造的相似三角形中，利用相似三角形的性质求得树的高度．
解答：
解：如图，过E作EH⊥AB于H，交CD于G；
则：CG=CD-EF=0.2米，EG=FD=4米，EH=BF=BD+DF=24米；
易知：△CEG∽△AEH，则有：
=
，
即：
=
，AH=1.2米；
∴AB=AH+BH=AH+EF=3米，
即树的高度为3米．
故答案为：3．
点评：此题是相似三角形的应用，正确作出辅助线构造相似三角形，是解题的关键．
解答：
解：如图，过E作EH⊥AB于H，交CD于G；则：CG=CD-EF=0.2米，EG=FD=4米，EH=BF=BD+DF=24米；
易知：△CEG∽△AEH，则有：
=，即：
=，AH=1.2米；∴AB=AH+BH=AH+EF=3米，
即树的高度为3米．
故答案为：3．
点评：此题是相似三角形的应用，正确作出辅助线构造相似三角形，是解题的关键．
练习册系列答案
相关题目
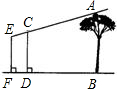如图所示，为了测量一棵树AB的高度，测量者在D点立一高CD=2米的标杆，现测量者从E处可以看到杆顶C与树顶A在同一直线上，如果测得BD=20米，FD=4米，EF=1.8米，则树的高度为
如图所示，为了测量一棵树AB的高度，测量者在D点立一高CD=2m的标杆，现测量者从E处可以看到杆顶C与树顶A在同一条直线上，如果测得BD=20m，FD=4m，EF=1.8m，则树AB的高度为
