题目内容
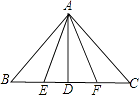
【题目】如图,△ABC中,AB=AC,∠BAC=45°,BD⊥AC,垂足为D点,AE平分∠BAC,交BD于F,交BC于E,点G为AB的中点,连接DG,交AE于点H, 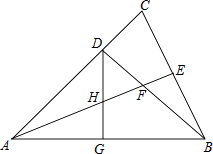
(1)求∠ACB的度数;
(2)HE= ![]() AF.
AF.
【答案】
(1)解:∵AB=AC,
∴∠ACB=∠ABC,
∵∠BAC=45°,
∴∠ACB=∠ABC= ![]() (180°﹣∠BAC)=
(180°﹣∠BAC)= ![]() (180°﹣45°)=67.5°
(180°﹣45°)=67.5°
(2)解:连结HB,
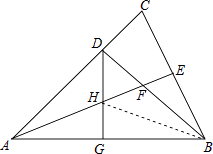
∵AB=AC,AE平分∠BAC,
∴AE⊥BC,BE=CE,
∴∠CAE+∠C=90°,
∵BD⊥AC,
∴∠CBD+∠C=90°,
∴∠CAE=∠CBD,
∵BD⊥AC,D为垂足,
∴∠DAB+∠DBA=90°,
∵∠DAB=45°,
∴∠DBA=45°,
∴∠DBA=∠DAB,
∴DA=DB,
在Rt△BDC和Rt△ADF中,
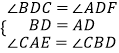
∴Rt△BDC≌Rt△ADF (ASA),
∴BC=AF,
∵DA=DB,点G为AB的中点,
∴DG垂直平分AB,
∵点H在DG上,
∴HA=HB,
∴∠HAB=∠HBA= ![]() ∠BAC=22.5°,
∠BAC=22.5°,
∴∠BHE=∠HAB+∠HBA=45°,
∴∠HBE=∠ABC﹣∠ABH=67.5°﹣22.5°=45°,
∴∠BHE=∠HBE,
∴HE=BE= ![]() BC,
BC,
∵AF=BC,
∴HE= ![]() AF
AF
【解析】(1)根据等腰三角形性质和三角形内角和定理求出即可;(2)证△ADF≌△BDC,推出AF=BC,求出HE=BE=CE,即可得出答案.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目