题目内容
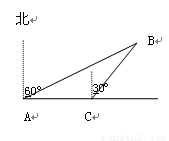
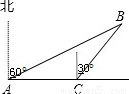
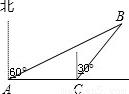
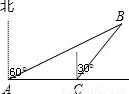
某民航飞机在大连海域失事，为调查失事原因，决定派海军潜水员打捞飞机上的黑匣子，如图所示，一潜水员在A处以每小时8海里的速度向正东方向划行，在A处测得黑匣子B在北偏东60°的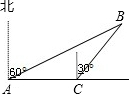
方向，划行半小时后到达C处，测得黑匣子B在北偏东30°的方向，在潜水员继续向东划行多少小时，距离黑匣子B最近，并求最近距离．
分析：最近距离即垂线段的长度．因此作BD⊥AC于D点，构造两个直角三角形，利用已知角的正切或余切分别表示出AD和CD，然后利用二者之间的关系列方程求解即可解决．
解答：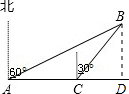
解：作BD⊥AC于D点．
在直角三角形ABD中，BD=tan∠BAC•AD=
AD，即AD=
BD；
在△BCD中，CD=tan∠CBD•BD=
BD，
∵AC=AD-CD=8×0.5=4，即
BD-
BD=4
∴BD=2
则CD=2，那么2÷8=0.25．
答：在潜水员继续向东划行0.25小时，距离黑匣子B最近，最近距离为2
．
解：作BD⊥AC于D点．在直角三角形ABD中，BD=tan∠BAC•AD=
| ||
| 3 |
| 3 |
在△BCD中，CD=tan∠CBD•BD=
| ||
| 3 |
∵AC=AD-CD=8×0.5=4，即
| 3 |
| ||
| 3 |
∴BD=2
| 3 |
答：在潜水员继续向东划行0.25小时，距离黑匣子B最近，最近距离为2
| 3 |
点评：“化斜为直”是解三角形的常规方法．
练习册系列答案
状元及第系列答案
同步奥数系列答案
相关题目
